МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО, МЛАДЕЖТА И НАУКАТА

ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА ПО АСТРОНОМИЯ

ХІV НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ

  Ученици от 7-8 клас

ТЕОРЕТИЧЕН ТУР

1 задача. Долината на скалите. Разполагате с красива снимка на нощен пейзаж със звездно небе. На езика на племето, живеещо по тези земи, мястото се нарича Tse Bii’ Ndzisgaii – Долината на скалите. Сравнете снимката със звездната карта.
• Приблизително в каква посока е гледал фотографът?
•Опитайте се да прекарате на снимката небесния екватор и да определите приблизително географската ширина на мястото.
•Най-яркото светило вляво на снимката е една от планетите. В кое съзвездие е тази планета?
•От вас не се иска да познаете точно коя е планетата. Само обяснете, за всяка от планетите от Слънчевата система, дали би могла или не би могла да бъде въпросното светило.

Решение:
От картата става ясно, че фигурата на митичния герой Орион се разполовява от небесния екватор и половината от нея е в северната, а другата половина е в южната небесна полусфера. На снимката се вижда, че северната част на съзвездието Орион, или главата на митичния ловец, е наляво, а южната част – надясно. Оттук заключаваме, че фотографът е гледал на изток, когато е правил снимката.
Сравняваме звездите на картата и на снимката и прекарваме небесния екватор върху снимката. Начертаваме и хоризонта.
Виждаме, че небесният екватор е наклонен на юг. Това означава, че мястото се намира в северното полукълбо на Земята. Измерваме с транспортир ъгъла между екватора и хоризонта и получаваме около 54°. За географската ширина на мястото получаваме северна ширина. Поради приблизителното прекарване на екватора и особеностите на проекцията на небесната сфера върху плоска равнина, при отклонение до 5° от този резултат решението следва да се приема за вярно.
Сравнението с картата показва, че ярката планета е в съзвездието Близнаци.
Коя би могла да е тази планета? Отново използвайки картата, можем да преценим, че тя е на около 20° над хоризонта. През съзвездието Близнаци преминава участък от еклиптиката, близък до точката на лятно слънцестоене. Той трябва да е почти успореден на небесния екватор. Следователно, ако Слънцето е на хоризонта, планетата би отстояла от него на ъгъл, съществено по-голям от 20°. Но очевидно снимката е направена в тъмна нощ (виждат се слаби звезди по цялото небе), когато Слънцето е доста под хоризонта. Следователно по направление на еклиптиката то е още по-далеч от планетата. Оттук заключаваме, че планетата със сигурност не е Меркурий, който при максимална елонгация се отклонява на около 28° от Слънцето.
За Венера, която при максимална елонгация е на около 47° от Слънцето, не можем да изключим или да потвърдим възможността да бъде обекта на снимката, при точността на данните, които имаме.
За външните планети няма проблем да бъдат в това положение на снимката. Марс и Юпитер могат да бъдат достатъчно ярки, за да изглеждат като въпросния обект, надвишавайки съществено по блясък ярките звезди от Орион . Планетата Сатурн също може да бъде ярка, но не толкова. Тя би била сравнима по блясък по-скоро със звездата  Ригел от Орион. Планетите Уран и Нептун не се виждат с невъоръжено око и дори няма защо да разсъждаваме за тях.
Накрая заключаваме, че ярката планета на снимката може да е Марс, Юпитер или Венера. В действителност, ако можехме да разгледаме цветния вариант на снимката, щяхме да видим червения оттенък на планетата, наподобяващ цвета на червения гигант Бетелгейзе от Орион. Така бихме стигнали до точното заключение, че планетата е Марс.

2 задача. Празник на Слънцето. В Стъкления град на Прекрасната планета най-веселият празник е Денят на високото Слънце. Тогава по пладне Слънцето е в зенита, а в полунощ центърът на видимия му диск е на хоризонта.
• Обяснете как е възможно това.
• Половин година по-късно (не земна година, а година на Прекрасната планета) се отбелязва друг празничен ден. Опишете как изглежда той. Обяснете своя отговор.
Рефракцията да не се отчита.

Решение (12 т.):
Прекрасната планета се върти около своята ос и затова нейното Слънце извършва видимо денонощно движение по небето. Нека с Р и Р′ отбележим северния и южния небесни полюси (Фиг. 1). В Деня на високото Слънце – най-веселия празник в Стъкления град – видимото движение на Слънцето става по паралел, минаващ през зенита Z и хоризонта. Понеже този паралел има за ос правата РР′, то височината  h  на северния небесен полюс над хоризонта и зенитното му отстояние ZP са равни. Следователно северният небесен полюс Р има височина над хоризонта  .  Това означава, че Стъкленият град трябва да е на географска ширина , ако върху Прекрасната планета въведем същите координати, както на Земята.
Щом Денят на високото Слънце се отбелязва като празник, значи през другите дни на годината по пладне Слънцето не се издига толкова високо. Денят на високото Слънце очевидно съответства на датата на лятно слънцестоене за полукълбото на Прекрасната планета, където се намира Стъкленият град. В точката на лятно слънцестоене Слънцето се намира най-далеч от небесния екватор – на 45°, както се вижда от чертежа. Това е и наклонът на екваториалната равнина за Прекрасната планета към нейната еклиптика (или нейната орбитална равнина).
Половин година по-късно Слънцето ще бъде в противоположната точка от еклиптиката – точката на зимно слънцестоене (Фиг. 2). Тогава то също ще е максимално далеч от небесния екватор, но в другата небесна полусфера за Прекрасната планета. Както показва чережът, на този ден Слънцето ще се покаже само на половина над хоризонта за много кратко време около пладне и пак ще се скрие под хоризонта. На тази дата за жителите на Стъкления град ще бъде най-дългата нощ, траеща почти цяло денонощие.

Фиг. 1

Фиг.2

3 задача.  Планета и луна. Скъпоценната луна обикаля около своята планета с период 12 дни. Едната й половина е диамантена, а другата – рубинена. При всяко пълнолуние Скъпоценната луна е обърната към планетата изцяло с диамантената си страна. При всяко новолуние също. Но при първа и последна четвърт Скъпоценната луна е обърната към планетата с точно противоположната си рубинена страна.
• Намерете трите възможно най-дълги периоди на околоосно въртене на Скъпоценната луна.
Разликата между сидеричния и синодичния период на Скъпоценната луна да се приеме за много малка и да не се отчита.

Решение (12 т.):
Нека приемем, че движението на Скъпоценната Луна около планетата става обратно на часовниковата стрелка. Схемата ни подсказва, че най-лесно ще намерим някакъв период на околоосно въртене на Скъпоценната Луна, ако предположим, че тя се върти по посока на часовниковата стрелка, или обратно на орбиталното си движение около планетата, като за всяка от четирите фази прави по четвърт завъртане. Наистина, от новолунието до първа четвърт ориентацията на рубинената и диамантената страна на Скъпоценната Луна се променя на четвърт оборот, или 90° (виж фигурата по-долу). Същото става и от първа четвърт до пълнолуние, от пълнолуние до последна четвърт и от последна четвърт до новолуние. Следователно периодът на въртене около оста на Скъпоценната луна, определен по този начин, е равен на орбиталния й перод, или на 12 дни. Разбира се, същите ориентации могат да се получат и ако луната на всеки четвърт оборот по орбитата се завърта допълнително на още един оборот около оста си, т.е. на един оборот и една четвърт.  Тогава за един орбитален период тя ще направи  1+4 = 5 завъртания. Тогава периодът и на околоосно въртене ще бъде  12/5 = 2.4  денонощия.   Или луната може да добави по два оборота около оста си за всяка четвърт обиколка по орбитата. Тогава за един орбитален период тя ще направи  1+8 = 9  завъртания,  а периодът й на околоосно въртене ще бъде 1 1/3 денонощия.
В повечето случаи, обаче, спътниците се въртят около осите си в същата посока, в която се движат по орбитите си около своите планети. Нека Скъпоценната луна се върти около оста си обратно на часовниковата стрелка. Тогава, след новолунието, за да застане с рубинената си страна към планетата, луната трябва да се завърти на ? оборот, после до пълнолунието още на ? оборот, до първа четвърт още на ? оборот и до новолунието още на ? оборот. Така за един орбитален период около планетата Скъпоценната Луна ще направи 4 ?3/4 = 3 завъртания около оста си. Следователно периодът й на въртене ще бъде 12 : 3 =  4 денонощия.  Ако разгледаме случая с по-бързо въртене в права посока, т.е. с едно допълнително завъртане на всеки четвърт оборот, ще се получи, че луната ще прави 7 завъртания около оста си, за един орбитален период. Следователно периодът й на околоосно въртене ще бъде 12/7 = 1 5/7  денонощия.
Останалите възможни случаи на въртене на луната около оста й се получават с добавяне на по още 4 допълнителни завъртания, на орбитален оборот, независимо от посоката на околоосно въртене. Очевидно е, че тогава периодът й на околоосно въртене ще се става все по-кратък.
Така получаваме, че трите възможни най-дълги периода на околоосно въртене на Скъпоценната луна са 12 денонощия, 4 денонощия и 2.4 денонощия.
Случаите на обратно орбитално движение на луната, са огледални на разгледаните, т.е. ще се получат същите периоди, но при обратни околоосни движения

ПРАКТИЧЕСКИ ТУР

Кометата Холмс. В периода 23 – 24 октомври 2007 г. не особено ярката комета Холмс претърпя изненадващо избухване и в рамките приблизително на 40 часа увеличи блясъка си около 500 000 пъти. Снимките, които са ви дадени, са направени от астронома Борислав Петров (Народна астрономическа обсерватория и планетариум „Н. Коперник” – Варна). На тях се вижда бързо разширяващата се кометна глава – обвивка от изхвърлените газове и прах.

• Определете размера на главата на кометата в километри на всяка снимка. Измервайте хордата, минаваща през звездообразното ядро на кометата и перпендикулярна на опашката, както е показано на изображението по-горе.
• Постройте графика на изменение на размера на главата с времето.
• Определете средната скорост на движение на изхвърлените от кометата частици в м/сек.
• С кое космическо тяло бихте сравнили размера на кометната глава на 13 ноември?

25.10.2007 г., 21:24 h, дългата страна на кадъра = 44.7′, разстояние от Земята 1.633 AU

06.11.2007 г., 19:18 h, дългата страна на кадъра = 44.7′, разстояние от Земята 1.620 AU

13.11.2007 г., 19:39 h, дългата страна на кадъра = 44.7′, разстояние от Земята 1.627 AU
На тази снимка кометното ядро се проектира близо до случайна звезда. Кометното ядро е леко вляво и надолу от близката звезда.

Под всяка снимка са дадени датата и моментът от време, мащаб за дългата страна на кадъра в дъгови минути и разстоянието до кометата в астрономически единици (AU).
1 AU = 150 000 000 км

Решение:
За да пресметнем мащаба на изображенията, измерваме дългата страна на един кадър. Тя е 165 мм и отговаря на 44.7′. Следователно мащабът е  44.7′ / 165 мм ≈  0.27′ / мм. Превръщаме времето  t  за всяка снимка в денонощия от момента 0 ч. на 25 октомври 2007 г. Измерваме размера  d  на главата на кометата в милиметри. Умножаваме го по мащаба, за да получим видимия ъглов размер  d′   на главата на кометата в дъгови минути. За линейния размер на главата на кометата можем да напишем:

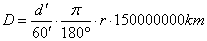
В тази формула последователно сме превърнали   d′  от минути в градуси и после в радиани. После умножаваме получения резултат по разстоянието  r  от Земята до кометата в километри.
Резултатите можем да представим в следната таблица:

Построяваме графика на изменението на размера на главата на кометата с времето.

За да намерим скоростта на разширение на главата на кометата, пресмятаме разликата между размера на главата по първата и по третата снимка и разделяме тази разлика на съответния интервал от време, превърнат в секунди. Получаваме: 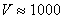м/сек. Тъй като изхвърлените от кометата частици се движат във всички посоки, за да намерим скоростта им относно кометното ядро, разделяме на две получената скорост. Средната скорост на движение на изхвърлените частици е около 500 м/сек.
Размерите, до които достига главата на кометата, са наистина впечатляващи. На 13 ноември тя е толкова голяма, че надвишава диаметъра на Слънцето, който е около 1 400 000 км. С това космическо тяло можем да я сравним.