|
МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО, МЛАДЕЖТА И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА ПО АСТРОНОМИЯ
ХV НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
ІІІ кръг
Ученици от 11-12 клас
ТЕОРЕТИЧЕН ТУР
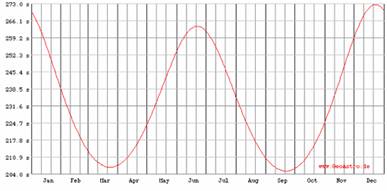
1 задача. Нека под продължителност на слънчевия изгрев да разбираме времето между момента, когато най-горната точка от видимия слънчев диск докосне хоризонта, и момента, когато най-долната точка от слънчевия диск се издигне на хоризонта. Дадената ви диаграма показва как се изменя продължителността на изгрева на Слънцето.
• Обяснете защо максимумите и минимумите на диаграмата се случват в съответните периоди от годината. Защо максимумите имат различна височина?
• Определете географската ширина на мястото, за което се отнася диаграмата. Считайте, че средният видим ъглов диаметър на Слънцето е 32.15 дъгови минути.
Решение:
За времето, в което продължава изгревът, Слънцето трябва да измине определено разстояние по небесната сфера при своето видимо денононщно движение. Продължителността на изгрева е различна в различни периоди на годината, защото видимата ъглова скорост на преместване на Слънцето е различна. Факторите, от които зависи тя, са няколко.
Поради движението си по еклиптиката, през годината Слънцето мени своята деклинация. Затова паралелите от небесната сфера, които то описва, са различни по размер. Ако считаме, че слънчевото денонощие винаги е равно точно на 24 часа, то само по тази причина видимата ъглова скорост на преместване на Слънцето по различните денонощни паралели ще бъде различна.
Най-бавно Слънцето ще се движи по паралелите, които описва в дните на лятното или зимното слънцестоене. Те отстоят на 23.5 от екватора и видимата ъглова скорост на Слънцето тогава ще бъде 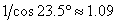 пъти по-малка (или с 9% по-малка), отколкото в дните на равноденствията, когато деклинацията му е нула и то описва денонощен паралел с размера на небесния екватор. Ето защо, както се вижда от диаграмата, има максимуми на продължителността на изгрева през юни и декември, когато са лятното и зимното слънцестоене, и минимуми през март и септември, когато са равноденствията.
Максимумите имат различна височина. Продължителността на изгрева около лятното слънцестоене е малко по-малка, отколкото около зимното слънцестоене. Обяснението е свързано с неравномерното движение на Земята по нейната елиптична орбита около Слънцето. Всъщност върху видимото движение на Слънцето от изток на запад, поради околоосното въртене на Земята, се наслагва видимото му годишно преместване в обратна посока – от запад на изток, поради орбиталното движение на Земята. Земята минава през перихелия на своята орбита в първите дни на януари. Тогава тя се движи с най-голяма скорост и е най-близо до Слънцето. Затова видимото годишно движение на Слънцето по еклиптиката е най-бързо и така най-силно се “забавя” видимото му денонощно движение по небето. Ето защо продължителността на изгревите около зимното слънцестоене е по-голяма, отколкото около лятното слънцестоене и максимумите имат различна височина. Освен това тогава, поради по-голямата близост на Земята до Слънцето, видимият ъглов диаметър на Слънцето е по-голям, което още повече увеличава продължителността на изгрева. Всъщност във времето около преминаването на Земята през перихелия факторът, свързан с видимия ъглов диаметър на Слънцето, играе значително по-голяма роля в увеличаването на продължителността на изгрева, отколкото изменението на видимата ъглова скорост на Слънцето.
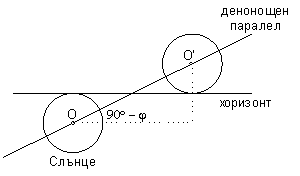
Най-просто ще решим въпроса с определяне на географската ширина на наблюдателния пункт, като разгледаме случая на изгрев около равноденствията. Графиката показва, че тогава продължителнастта на изгрева е приблизително 206 секунди (вземаме средната продължителност от двата минимума на графиката). Тогава Слънцето се движи по денонощен паралел с размерите на небесния екватор и датите са далеч от преминаването на Земята през перихелия и през афелия, така че не се налага да се въвеждат коригиращи коефициенти, поне за точността, с която работим. Денонощният паралел на Слънцето, съвпадащ с небесния екватор, е наклонен към хоризонта на ъгъл 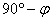 , където φ е търсената географска ширина. За времето, през което продължава изгревът, центърът на Слънцето изминава път ОО&prime. Можем да го намерим чрез следната пропорция:
24 h – 360°
206 s – OO′
-------------------------------
OO’ ≈ 0.858′
Както се вижда от чертежа, за време 206 s във вертикална посока центърът на Слънцето изминава разстояние колкото видимия ъглов диаметър на Слънцето δo . Оттук намираме:
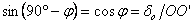
φ = 51.37°
Критерии за оценяване (общо 16 т.):
За обяснение защо минимумите и максимумите се случват през съответните периоди от годината – 4 т.
За обяснение на различната височина на двата максимума – 4 т.
За подходящ избор на период през годината, данните от който да се използват за определяне на географската ширина и обяснение – 2 т.
За определяне на продължителността на изгрева, необходима за пресмятанията, от графиката – 1 т.
За правилна логическа постановка на решението на въпроса за ширината – 2 т.
За правилни пресмятания – 2 т.
За верен числен отговор – 1 т.
2 задача. Тъмни небеса. Тайната звезда е скрита в плътен космически облак. Лъчението на звездата е отвяло веществото от централните части на облака към периферията. В това пространство, изпълнено само с много разредена материя, около Тайната звезда практически без съпротивление по кръгови орбити се движат Пясъчната и Водната планета. Поради космическия облак, обаче, от повърхността на планетите нощем не може да се види нито една звезда. Учените от Водната планета вече са развили много добре теорията за гравитацията и познават всички закономерности, които следват от нея и се отнасят до движението на космическите тела. Освен това, те системно наблюдават Пясъчната планета, която е вътрешна за тях.
• Предложете метод, по който учените от Водната планета могат да определят отношението на радиусите на орбитите на двете планети и орбиталния период на своята планета. Опишете какви наблюдения трябва да се направят. Обосновете метода чрез алгебрични пресмятания.
• След като са пресметнали величините, посочени в първото подусловие, астрономите от Водната планета искат да определят и масата на Тайната звезда. Опишете само качествено какви допълнителни наблюдения трябва да направят, какво ще определят от тях и как ще намерят масата на своята звезда.
Решение:
Ако в небето на една планета не се виждат звезди, астрономите там не могат да проследяват видимото движение на другите планети от своята система и на своето слънце на фона на звездното небе. Те единствено могат да наблюдават относителните движения на планетите и слънцето. Понеже Пясъчната планета е вътрешна за Водната планета, учените от Водната планета могат да наблюдават редуващите се моменти на съединения и максимални елонгации. От тези наблюдения те могат да измерват ъгловото отстояние φ на Пясъчната планета от Тайната звезда при максимална елонгация.
Това може да им помогне да определят съотношението на орбиталните радиуси на двете планети. Както се вижда от чертежа:
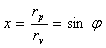
Извънземните същества могат да определят от наблюденията си и синодичния период на планетата TS . Щом познават така добре теорията за гравитацията, можем да предположим, че знаят и ІІІ закон на Кеплер. Въз основа на това могат да се напишат следните уравнения:
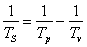
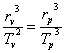
където Tp и Tv са сидеричните периоди на Пясъчната и Водната планета. От тези уравнения получаваме:
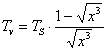
Всъщност, астрономите от Водната планета могат да определят и орбиталния период на Пясъчната планета, макар това да не се иска в условието на задачата:
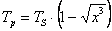
За да определят масата М на Тайната звезда, на извънземните астрономи им трябва да знаят само още поне един от радиусите на планетните орбити. Тогава те могат да напишат ІІІ закон на Кеплер във вида:
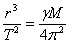
където r е орбиталният радиус на която и да е от планетите, а Т е нейният сидеричен период. Оттук се получава:
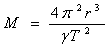
За да определят разстоянията на планетите до Тайната звезда, астрономите могат да наблюдават пасаж на Пясъчната планета по диска на Тайната звезда. За целта те трябва предварително да са определили размерите на собствената си планета и да наблюдават пасажа от най-малко два раздалечени един от друг пункта. При наблюденията от двата пункта Пясъчната планета ще се проектира на различни места върху диска на Тайната звезда. По това паралактично отместване, и като се знае разстоянието между двата наблюдателни пункта, може да се определи разстоянието от Водната до Пясъчната планета по време на пасажа. После лесно може да се определят и орбиталните радиуси на двете планети.
Критерии за оценяване (общо 15 т.):
За разбиране на проблемите пред астрономите при липса на звезди и описание на идеята за метода за определяне на съотношението на орбиталните радиуси – 2 т.
За математическо представяне на метода – 2 т.
За правилно получаване на отношението на радиусите – 1 т.
За математическо представяне на метода за определяне на орбиталния период на Водната планета – 5 т.
За правилно пресмятане на периода – 1 т.
За математическо представяне на начина за определяне на масата на звездата – 2 т.
За качествено описание на начина за определяне на разстояния в планетната система – 2 т.
3 задача. Планетата около двойна звезда. Преди няколко месеца, с помощта на космическия телескоп Kepler,е открита за първи път планета около двойна звезда. При това звездата се наблюдава като затъмнително-променлива. По-ярката звезда е от спектрален клас К и е с радиус приблизително 0.65 слънчеви радиуса. Планетата Kepler-16b е с размерите на Сатурн и се движи едновременно около двете звезди, като преминава пред всяка една от тях. На кривата на блясъка се виждат както затъмненията на звездите една от друга, така и пасажите на планетата пред дисковете на звездите. В четири допълнителни диаграми, в по-подходящ мащаб, са показани примери на такива затъмнения и пасажи.
• Каква звезда е втората компонента на двойната звезда? Защо?
• Коя допълнителна крива на блясъка за какъв вид явление се отнася? Обяснете защо. Обяснете формата на кривите на блясъка при всеки вид затъмнение. Коментирайте качествено както продължителността на затъмненията, така и амплитудата на всяка крива на блясъка. Нарисувайте една вероятна позиция на телата при максимална фаза за всеки вид затъмнение.
• На горната крива на блясъка са дадени затъмненията за дълъг период от време. Всяко затъмнение е посочено със стрелка. Кое затъмнение за какъв вид явление се отнася? Какви са приблизителните периоди на звездите и планетата при тяхното движение по орбитите им?
Кривите на блясъка са дадени не в относителни звездни величини, а в относителни потоци светлина.
Решение:
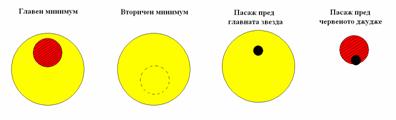
На горната крива на блясъка се вижда, че има два типа минимуми, които са типични за двойна звезда. Това са дълбоките минимуми, които се повтарят през точно определен интервал от време, и в средата на всеки интервал минимуми, които са много по-плитки (с много по-малка амплитуда). На цветната крива те са означени съответно със син и с жълт цвят. При по-дълбоките минимуми се затъмнява по-горещата звезда. Един индивидуален минимум е показан на втория ред, отляво. Виждаме, че промяната в потока светлина е плавен. Минимумът е заоблен. За разлика от него, вторичният минимум, чиято форма е показана вдясно от първичния, има плосък участък, който подсказва, че в този интервал от време ние виждаме само главната звезда, а по-малката по размери звезда е скрита зад нея за интервал от време, равен по продължителност на плоския участък. Амплитудата на вторичния минимум е само един и половина процента от общия блясък на системата и следователно втората звезда е не само по-малка по размери от първата, но и съществено по-слаба по блясък, а следователно по-студена и по-червена от главната звезда. Оттук правим извода, че втората компонента на двойната звезда е червено джудже.
Първият показан минимум е получен от затъмнение на главната звезда от вторичната, която е по-малка и по-студена. Виждаме че блясъкът първоначално спада сравнително равномерно, след това има заоблен минимум, след което блясъкът се покачва. Не се наблюдава равен участък, подобно на равния участък на вторичния минимум. Това се дължи на потъмнението към края на диска на главната звезда, а прекалено острият минимум подсказва и че затъмнението не е централно. Вторичният компонент преминава недалеч от края на звездата, поради което се движи в област силно повлияна от потъмнението към края на диска.
При вторичния минимум забелязваме, че равният участък е малко по-дълъг от една трета от продължителността на целия минимум. Следователно другите два участъка от кривата са малко по-къси от една трета от целия минимум. Знаейки вече, че затъмнението не е централно и че звездата се скрива и открива, пресичайки наклонен участък от края на диска на главния компонент, може да заключим, че най-вероятно вторичният компонент е около три пъти по-малък по размери от главния.
При внимателно сравнение на двата минимума забелязваме, че тяхната продължителност е различна. Ако орбитите на звездите са кръгови, това не е възможно. Следователно орбитите са елипси, като апсидната линия на орбитите е насочена приблизително към наблюдателя. Затъмненията стават при преминаване на звездите през периастъра и апоастъра на техните орбити. Тъй като главният минимум е по-продължителен, то тогава звездите се намират недалеч от апоастъра на техните орбити. Във вторичния минимум, който е по-кратък, звездите са недалеч от периастъра на техните орбити и скоростта им е по-голяма.
Следващите два минимума са фотометрични профили на пасажа на планетата върху дисковете на звездите. Третият минимум (зеленият) се е получил вследствие на пасаж на планетата по диска на главната звезда. Той е по-продължителен, защото орбитата на планетата е по-голяма от орбитите на звездите. Затова планетата се движи по-бавно от звездите. Все пак разликата не е много голяма. Причината за това е едно много странно обстоятелство. Въпреки предварителните представи, че около двойна звезда не може да има планета на стабилна орбита с радиус по-малък от седемкратното разстояние между компонентите на двойната звезда се оказа, че планетата Kepler-16b се намира на двойно по-малко разстояние, само три пъти и половина от разстоянието между звездите. Формата на кривата е класическа за пасаж на планета върху диска на звездата. В началота има рязък спад на блясъка (макар и неголям по амплитуда) дължащ се на навлизането на диска на планетата пред диска на звездата. След това следва широк плавен участък който се формира при движението на планетата пред диска на звездата и чиято форма се определя от потъмнението към края на диска на звездата. Тъй като планетата преминава последователно и пред двете звезди, то тя вероятно пресича диска на главната компонента някъде между центъра и края на диска на звездата. Това също допринася за неголямата продължителност на затъмнението. Освен това този индивидуален минимум, както може да видим от горната крива на блясъка, е позициониран след главен минимум на двойната звезда, когато компонентите са преминали през апоастъра на своите орбити и главната компонента на двойната звезда се движи, макар и с относително неголяма скорост, в посока противоположна на движението на планетата по нейната орбита. Това, че планетата е по-малка по размери от звездите, също допринася минимумът да е по-кратък от очакваното. Освен това може да обърнем внимание на една лека вълничка след минимума на иначе много гладката крива. Тази неравномерност ни навежда на мисълта за наличието на петна по диска на главната компонента. Наистина, ако планетата застане точно пред петно върху диска на планетата, тя ще блокира по-малко светлина, а ако преди това мине пред факелно поле, тя ще блокира малко повече светлина от средното. (Както ще видим, наличието на петна ще установим и при анализа на общата крива на блясъка).
Последната индивидуална крива на минимум, червената, на пръв поглед изглежда много странно. Тя е много кратка и с много малка амплитуда – само една хилядна от общия блясък на системата. Това се обяснява с преминаването на планетата пред диска на втората компонента – червеното джудже. Краткостта на затъмнението се дължи преди всичко на малките размери на вторичния компонент на двойната звезда. Приносът на червеното джудже към общия блясък на системата е много малък – половин процент. Затова затъмняването на част от диска му води до много малки промени в общия блясък на системата. Формата на минимума ни навежда на мисълта, че затъмнението не е пълно. Планетата навлиза пред диска на малката звезда странично, като част от нея остава извън диска на звездата. При максималната фаза планетата с вътрешния край на диска си, за много кратък интервал от време, блокира част от по-ярката централна област от звездата. Това води до кратък остър минимум, какъвто наблюдаваме.
На горната крива на блясъка е дадена промяната в блясъка на системата за продължителен период от време, около 600 дни. Най-дълбоките минимуми, отбелязани със син цвят, са главните минимуми. Четвъртият главен минимум липсва. Вероятно не е наблюдаван по технически причини. Вторичните минимуми са почти точно между главните. Отбелязани са с оранжев цвят. Това, че са по средата, между главните минимуми, показва, че апсидната линия е ориентирана по направление към наблюдателя.
Има три двойки пасажи отбелязани със зелен и червен цвят. Червените изглеждат като точки върху кривата на блясъка поради малката си амплитуда. Търсете червените стрелки по абцисата, които ги посочват. Виждаме, че се наблюдава известна симетрия в разпределението на пасажите спрямо минимумите на двойната звезда. Първата двойка пасажи е преди вторичния минимум, втората – след, третата отново е преди вторичния минимум. Това вероятно се дължи на резонанси в периодите на телата от звездната система. Зелените имат амплитуда приблизително равна на амплитудата на вторичните минимуми. Въпреки че планетата е по-малка, тя не дава принос към блясъка на системата, за разлика от червеното джудже.
Забелязва се и нещо много интересно. Общата крива на блясъка е вълнообразна. Това се дължи на наличието на големи петна и групи от петна по главната звезда на системата. Вижда се, че някои от минимумите са повдигнати или спуснати в зависимост от това в каква част от вълните са се случили. Както видяхме преди, наличието на петна оказва влияние и върху формата на кривите на пасажите на планетата по главната звезда.
Отчитаме моментите на минимумите по абцисата за по-голям интервал от време и за периода на двойната звезда получаваме – 41.1 денонощия. За периода на пасажите – 226.5 денонощия.
И двете стойности са много близки до получените от професионалните астрономи, изследващи звездата.
Критерии за оценяване (общо 20 т.):
За правилни разсъждения по въпроса каква е втората зведа – 3 т.
За правилно заключение за вида на тази звезда – 1 т.
За правилни разсъждения върху формата, амплитудата и продължителността на графично представените минимуми 4 т.
За правилни заключения по отъждествяване на графиките със съответните минимуми – 2 т.
За правилно скициране на взаимните положения на компонентите – 4 т.
За отъждествяване на вида на затъмненията по горната графика – 4 т.
За определяне на периодите – 2 т.
ПРАКТИЧЕСКИ ТУР
Практическа задача. Юпитер и спътникът Йо.
Дадени са ви две снимки, направени на 28 септември 2011. Фотографирани са два последователни момента от преминаването на сянката на спътника Йо по видимия диск на планетата Юпитер. На първата снимка самият спътник Йо се вижда вляво от Юпитер. На втората снимка спътникът се проектира върху Юпитер и е посочен със стрелка.
На 29 октомври 2011 г. Юпитер е бил в противостоене.
• Като използвате снимките, направете необходимите измервания и построения и пресметнете приблизително масата на Юпитер. Опишете вашия метод на работа.
Справочни данни:
Радиус на Юпитер 71 500 км,
Гравитационна константа 6.67×10-11 м3/кг.с2
Радиус на орбитата на Юпитер 5.2 AU
Орбитален период на Юпитер 11.862 год.
1:23 h UT
2:53:58 h UT
Решение: За да получим под какъв ъгъл Слънцето осветява Юпитер и спътниците му на 28 септември 2011г. относно линията Земя – Юпитер, използваме информацията за момента на опозиция. Ще фиксираме направлението Слънце – Юпитер в момента на противостоене, ще се върнем 31 дни назад и ще пресметнем ъгъла между направленията Слънце – Юпитер и Земя – Юпитер.
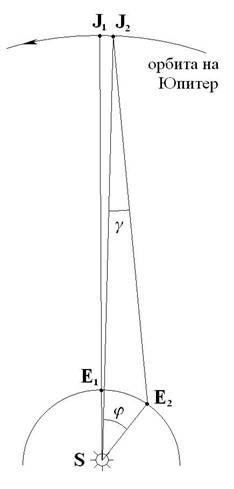
Нека в момента на опозиция, на 29 октомври 2011 г., Юпитер се намира в точка J1, а Земята е в точка E1. На 28 септември, 31 дни по-рано, Юпитер и Земята ще са съответно в точки J2 и E2. За да решим задачата, трябва да намерим ъгъл g, който е фазовият ъгъл на Юпитер в момента на наблюденията. За целта първо намираме ъгъл φ.
Определяме на какъв ъгъл се е завъртяла Земята по орбитата си от E1 до E2 и от този ъгъл изваждаме ъгъла, на който се е завъртял Юпитер за същото време. Ъглите на завъртане намираме като разделим 360° на броя на дните в годината за съответната планета, след което умножаваме по 31 дни. Получаваме ъгъла на завъртане на всяка една от планетите. За Земята получаваме, че ъгълът на завъртане е 29°.54, а за Юпитер - 2°.50. Търсеният ъгъл φ се получава като извадим втория ъгъл от първия. Получаваме:
φ = 27°.04 ≈ 27°
Прилагаме косинусовата теорема за триъгълник J2SE2 и намираме разстоянието J2E2. След това за същия триъгълник прилагаме синусовата теорема и намираме ъгъл γ ≈ 6°. Това е ъгълът, под който Слънцето осветява спътниците на Юпитер спрямо линията Земя – Юпитер.
За реперни точки използваме сенките на спътника Йо върху повърхността на Юпитер. Ще прекараме линиите Слънце – Йо – сянка на Йо, като използваме определения по-горе ъгъл γ. След това ще ги пресечем с линии успоредни на линията Земя – Юпитер. Пресечните точки ще ни дадат две положения на спътника по неговата орбита. Провеждаме измервания върху снимките. Измерваме екваториалния диаметър на Юпитер.
Пресмятаме радиуса на изображенията на планетата. Измерваме отстоянието на изображенията на спътника и на сенките на спътника от линията, свързваща двата полюса на планетата и перпендикулярна на неговия екватор. Намираме отношенията на отстоянията на сенките към радиуса на изображението на Юпитер. Построяваме в подходящ мащаб полуокръжност на лист милиметрова хартия. Това е обърнатата към наблюдателя половина от екватора на планетата. Върху линията, определена от диаметъра на тази полуокръжност, нанасяме в съответния мащаб проекциите на сенките на Йо S1′ и S2′, отговарящи на измерванията ни по снимките. От точките S1′ и S2′ начертаваме линии, перпендикулярни на диаметъра на полуокръжността и насочени към земния наблюдател. Тези линии пресичат полуокръжността в точки S1′ и S2′ , съответстващи на положенията на сенките на Йо върху повърхността на Юпитер. (На дадените снимки сенките не са на екватора, но това се дължи на наклона на оста на планетата и на орбитите на спътниците към плоскостта на орбитата на Юпитер. Този наклон, щом виждаме сенките далеч от екватора, е преимуществено в направление към наблюдателя. Тогава положението на сенките се премества в посока перпендикулярна на екватора, без да се измества съществено встрани.) Приемаме, че направлението към наблюдателя е успоредно на линиите на милиметровата хартия. От сенките прекарваме прави линии под ъгъл γ спрямо направлението към земния наблюдател.
Проектираме положенията на изображенията на спътника I1′ и I 2′ върху линията на среза на екватора на Юпитер, използвайки подобни отношения от предоставените снимки. От тези проекции на спътника прекарваме прави линии, успоредни на направлението към наблюдателя, до пресичането им с наклонените линии от сенките на спътника. Пресечните точки I1′ и I 2′ са две положения на спътника върху неговата орбита. Намираме средното разстояние до центъра на планетата. Сравняваме с радиуса на построения полуекватор на планетата и преминаваме към реални единици, използвайки дадения ни в условието радиус на планетата. Получаваме, че радиусът на орбитата е:
R = 451 000 km
Измерваме ъгъла с връх в центъра на Юпитер О и лъчи към двете положения I1 и I 2 на Йо по орбитата му. Знаем какво време е изминало между двете положения на спътника. Оттук намираме периода на орбитално движение на Йо. Получаваме:
T = 168000s = 1d 22h 40m
Прилагаме пълната форма на третия закон на Кеплер за Юпитер и параметрите на орбитата на Йо:
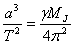
и получаваме за масата на Юпитер:
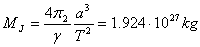
Стойностите за радиуса на орбитата и за периода не са много точни поради това, че приехме орбитите на двете планети за кръгови и движението им по орбитите за равномерно, но неточностите се компенсираха във формулата за масата и стойността, която получихме за нея, се отличава от истинската изключително малко.
Критерии за оценяване (общо 20 т.):
За математическа обосновка на метода за определяне на ъгъла, под който Слънцето осветява Юпитер спрямо линията Земя-Юпитер – 4 т.
За правилно определяне на този ъгъл – 2 т.
За обяснение на метод, по който да се построят точки от орбитата на Йо чрез измервания на положенията на спътника и неговята сянка на снимките – 5 т.
За прецизно приложение на метода и определяне на радиуса на орбитата на спътника около Юпитер – 3 т.
За построения и измервания с цел да се определи орбиталния период на Йо и за получаване на този период – 4 т.
За определяне на масата на Юпитер – 2 т.
|
|
