|
МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО, МЛАДЕЖТА И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА ПО АСТРОНОМИЯ
ХІV НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
ІІІ кръг
Ученици от 11-12 клас
ТЕОРЕТИЧЕН ТУР
1 задача. Астроном отшелник. Вие работите по дългосрочна програма с 10-метровия микровълнов телескоп на Южния полюс и изследвате разпределението на далечните купове от галактики в пространството. Въпреки антарктическия студ, по време на изгрева на Слънцето вие се разхождате покрай телескопа и се любувате на гледката. Забелязвате, че в даден момент Слънцето се намира на хоризонта точно по посока от жилищната постройка към телескопа. В този момент центърът на видимия слънчев диск пресича хоризонта. Нека приемем линията от постройката към телескопа за основна.

• В какви направления спрямо основната линия ще са точките от хоризонта, които ще пресече центърът на видимия слънчев диск при следващите четири изгрева? Пресметнете отклоненията от основната линия в градуси.
• При някакъв изгрев на Слънцето, едновременно с него изгрява и Луната. Приблизително в каква фаза трябва да е Луната тогава? Дайте качествен отговор и го обяснете.
Рефракцията да не се отчита и в двете подусловия. Снимката е само илюстрация и сенките, които се виждат на нея, не са част от решението на задачата.
Решение:
При нас Слънцето изгрява и залязва поради видимото си денонощно движение по небето, дължащо се на въртенето на Земята около нейната ос. На полюсите изгревът на Слънцето става поради видимото му годишно движение по еклиптиката. На южния полюс това се случва, когато Слънцето пресича небесния екватор от северната към южната небесна полусфера, т.е. при преминаването му през есенната равноденствена точка около 23 септември. Следващият изгрев се случва при следващото преминаване на Слънцето през тази точка, или точно след една тропична година. В тропичната година има 365.24219 слънчеви денонощия. Една тропична година след първия изгрев на Слънцето Земята ще е направила 365 пълни завъртания около оста си по отношение на посоката към Слънцето и още 0.24219 части от пълното завъртане, или  . Гледано от южното полукълбо, Земята се върти около оста си по часовниковата стрелка. Затова там видимото денонощно въртене на Слънцето е обратно на часовниковата стрелка. Оттук заключаваме, че при втория си изгрев Слънцето ще пресече хоризонта на 87.19° обратно на часовниковата стрелка, или наляво от основната линия от сградата към телескопа. При следващите три изгрева то ще се появи съответно на . Гледано от южното полукълбо, Земята се върти около оста си по часовниковата стрелка. Затова там видимото денонощно въртене на Слънцето е обратно на часовниковата стрелка. Оттук заключаваме, че при втория си изгрев Слънцето ще пресече хоризонта на 87.19° обратно на часовниковата стрелка, или наляво от основната линия от сградата към телескопа. При следващите три изгрева то ще се появи съответно на  , ,  и и  обратно на часовниковата стрелка от основната линия. Бихме могли да кажем, че накрая, при петия си изгрев Слънцето ще бъде само на обратно на часовниковата стрелка от основната линия. Бихме могли да кажем, че накрая, при петия си изгрев Слънцето ще бъде само на  надясно, или по часовниковата стрелка от основната линия. надясно, или по часовниковата стрелка от основната линия.
На полюса изгревът на Луната става поради орбиталното й движение около Земята. Луната може да изгрее едновременно със Слънцето, например, при слънчево затъмнение. Тогава нейната фаза е близка до новолуние. Но лунната орбита има лек наклон към еклиптиката. Затова може да се случи Луната да пресече небесния екватор заедно със Слънцето, когато фазата й е малко преди или малко след новолуние. Най-голямо отклонение на фазата от новолунието може да има, когато Луната е в някоя от точките по лунната орбита, които са най-отдалечени от еклиптиката. Обаче, за разлика от Слънцето, не е достатъчно Луната да пресече небесния екватор, за да изгрее за някой от полюсите. Впрочем Слънцето също не изгрява там, намирайки се точно на небесния екватор. В случая то трябва да е на 8.76″ южно от екватора, колкото е видимият ъглов размер на земния радиус, гледан от Слънцето. Разбира се, без да отчитаме рефракцията. Земният радиус, гледан от Луната, се вижда под ъгъл 0.95°. Следователно Луната трябва да слезе на този ъгъл южно под небесния екватор, за да изгрее за наблюдател на Южния полюс. Фазата може да е малко преди или малко след новолуние, или новолуние, в зависимост от това, колко се отклонява орбитата на Луната от еклиптиката в този участък и в каква посока е Луната относно Слънцето.
2 задача. Пасаж на Юпитер. В търсене на астероиди троянци по орбитата на Сатурн, вие излитате с космически кораб от Земята на далечно пътешествие. Космическият кораб излита по посока на орбиталното движение на Земята и лети по икономична траектория – елипса с перихелий върху земната орбита и с афелий върху орбитата на Сатурн. Когато достигате афелия на вашата орбита, вие наблюдавате красиво явление – преминаване (пасаж) на планетата Юпитер по диска на Слънцето.
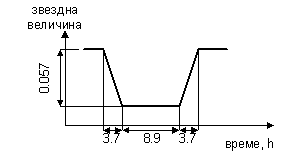
• Представете схематично кривата на изменение на блясъка на Слънцето по време на пасажа.
• Пресметнете и означете върху нея интервалите от време между характерните моменти – І, ІІ, ІІІ и ІV контакт (моментите, когато Юпитер започне да навлиза на фона на слънчевия диск, когато вече напълно е навлязъл, когато започне да излиза от слънчевия диск и когато напълно е излязъл.
• С колко се изменя звездната величина на Слънцето?
Смятайте, че по време на пасажа скоростта на вашия кораб е равна на скоростта му в афелий и не се променя по време на наблюдението.
Решение:
За да направим исканите в задачата пресмятания, първо трябва да определим скоростта на нашия кораб в афелия на орбитата му. Означаваме разстоянията му до Слънцето в перихелий и афелий съответно с rp и ra . Тези разстояния всъщност са равни на радиусите на земната орбита и на орбитата на Сатурн около Слънцето. Означаваме с М масата на Слънцето и с γ гравитационната константа. Използваме закона за запазване на енергията и ІІ закон на Кеплер:
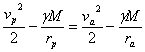
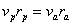

След известни преобразувания получаваме:
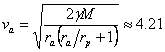 км/сек км/сек
Продължителността на пасажа ще определим, като преминем в координатна система, неподвижно свързана с нашия кораб. В тази система Слънцето се движи относно нас със корост – va , а Юпитер със скорост vj – va , където 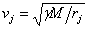 е скоростта, с която Юпитер се движи по своята орбита с радиус rj . Ъгловата скорост, с която става видимото преместване на Слънцето по небето за нас е е скоростта, с която Юпитер се движи по своята орбита с радиус rj . Ъгловата скорост, с която става видимото преместване на Слънцето по небето за нас е 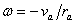 , ъгловата скорост на Юпитер е , ъгловата скорост на Юпитер е 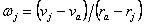 . Тук приемаме, че ъгловата скорост на Юпитер не се променя по време на пасажа, което, предвид малките ъглови размери на Слънцето, е допустимо приближение. Видимата ъглова скорост, с която Юпитер с движи на фона на слънчевия диск, е: . Тук приемаме, че ъгловата скорост на Юпитер не се променя по време на пасажа, което, предвид малките ъглови размери на Слънцето, е допустимо приближение. Видимата ъглова скорост, с която Юпитер с движи на фона на слънчевия диск, е:
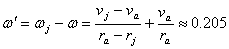 ′/час ′/час
Трябва да пресметнем и видимите от нашия кораб ъглови диаметри на Слънцето и на Юпитер. Те са съответно:
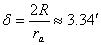 , където R е линейният радиус на Слънцето, , където R е линейният радиус на Слънцето,
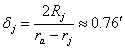 , където Rj е линейният радиус на Юпитер. , където Rj е линейният радиус на Юпитер.
Оттук за интервалите между І и ІІ контакт, ІІ и ІІІ контакт и ІІІ и ІV контакт получаваме:
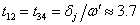 часа часа
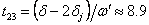 часа часа
Означаваме с Е0 осветеността, която създава Слънцето, без Юпитер да се проектира на фона на неговия видим диск, а с Е – осветеността, която то създава по време на пасажа. Отношението на двете осветености ще е равно на отношението на площта на видимия слънчев диск без да го закрива планетата и светещата част от площта му, когато върху него е проектирана планетата:
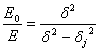
Изменението на звездната величина на Слънцето по време на пасажа ще бъде:
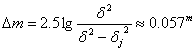
Накрая можем да представим всичко това схематично на една графика:
3 задача. Шега на «боговете». Земята обикаля около Слънцето по елипса, в един от фокусите на която се намира Слънцето. В другия фокус, както знаем, няма нищо. Да предположим, че нашата планета случайно влиза в полезрението на галактична цивилизация с високо развити космически технологии. Проявявайки също толкова мащабно чувство за хумор, цивилизацията мигновено премества Слънцето от единия в другия фокус на земната орбита.
• Опишете качествено и обяснете какво ще се случи с орбитата на Земята, ако в момента на преместването тя е в перихелия на сегашната си орбита. А ако е в афелия?
• Съществува ли точка от земната орбита, в която ако се намира Земята в момента на преместването, формата на орбитата не се променя? Какво, обаче, се променя тогава?
Влиянието на другите планети да не се отчита.
Решение: Тъй като земната орбита е много близка до кръговата, двата фокуса на елипсата са близо един до друг. Същественото в случая е, че когато Земята е в перихелий, тя е най-близо до този фокус на елиптичната орбита, в който се намира Слънцето. Тогава, освен че Земята е най-близо до Слънцето, там орбиталната й скорост е максимална. Скоростта в перихелий е по-голяма от кръговата скорост за това разстояние от Слънцето. Обратно, скоростта на Земята в афелия на орбитата й е минимална. Скоростта там е по-малка както от кръговата скорост за афелийното разстояние, така и от перихелийната скорост. Ако в момента в който Земята преминава през перихелия на орбитата си, Слънцето “прескочи” в другия фокус, изведнъж ще се окаже, че Земята е на афелийно разстояние от Слънцето, но с перихелийна скорост. Това означава, че тя ще започне да се движи около Слънцето по по-външна орбита, която ще включва в себе си предишната орбита, като ще се докосва до нея само в една точка – тази точка, в която се е намирала в момента на смяната, т.е. в перихелия на старата орбита. Голямата полуос на орбитата ще е по голяма и следователно и периодът на обикаляне ще е по-дълъг.
Ако в момента на преместването на Слънцето Земята се намира в афелия на своята орбита, тя изведнъж ще се окаже на перихелийно разстояние от него, но с афелийна скорост. Афелийната скорост е по-малка от перихелийната и Земята ще започне да се движи по орбита по-близка до Слънцето, която ще се докосва до предишната орбита в точката в която е станала смяната, т.е. в афелия на старата орбита. Голямата полуос на орбитата и периодът на обикаляне около Слънцето ще са по-малки.
Има две точки по орбитата на Замята, обаче, в които тя се движи с еднаква скорост, но в противоположни посоки. Тези точки се намират там където малката ос допира орбитата и я разделя на две еднакви части, полуелипси, в едната от които се намира перихелият на орбитата, а в другата – афелият на орбитата. Въпреки, че по дължина и форма двете части на орбитата са еднакви, те се изминават за различно време. Половината орбита, съдържаща перихелия, се изминава за по-кратко време отколкото другата половина, която съдържа афелия. Ако в момента на смяната Земята се намира в една от двете точки, то прескачането на Слънцето от единият фокус в другия няма да промени размерите и формата на орбитата. Обаче ще настъпи друга интересна промяна в движението на Земята. Нека тя е преминала перихелия и е на средата на пътя към афелия на орбитата си. Прескачането на Слънцето ще доведе до това, че перихелият и афелият ще си разменят местата. На Земята, която ще продължи движението си по орбитата, ще й се наложи отново да премине през тази половина от орбитата, която съдържа перихелия. Заедно с всички последствия от това – отново по-бързо движение и повече топлина от Слънцето. След това всичко ще продължи както и преди смяната. Само, че през лятото, в началото на юли, вместо да преминава през афелия Земята ще преминава през перихелия на орбитата си и обратно – през зимата, в началото на януари, вместо да преминава през перихелия Земята ще преминава през афелия на орбитата си. А годината, в която се е случила смяната, ще бъде по-къса от другите години. Разликата в продължителността на годините ще е равна на разликата във времената, за които Земята изминава двете, еднакви по големина и форма, но различни по средна скорост, половини на земната орбита.
Ако смяната стане, когато на Земята и предстои да навлезе в половината на орбитата съдържаща перихелия, ще се случи обратното – ще се повтори преминаването през афелия на орбитата и ще преживеем най-дългата, затова пък малко по-студена, година. Всички останало е аналогично на предишния случай.
Справочни данни:
Радиус на земната орбита – 150 × 106 км.
Маса на Слънцето – 2 × 1030 кг
Радиус на Слънцето – 696 000 км
Гравитационна константа – 6.67 × 10-11 м3 /кг.сек-2
Радиус на орбитата та Юпитер – 5.20 астрономически единици
Радиус на Юпитер – 71 500 км
Радиус на орбитата на Сатурн – 9.54 астрономически единици
ПРАКТИЧЕСКИ ТУР
Кратерът Коперник. Разполагате със снимка на Луната и изображение на кратера Коперник, което представлява увеличен участък от същата снимка. Направете необходимите построения и измервания и определете приблизително височината на кръглия вал на кратера.
Радиусът на Луната е 1738 км.
Решение:
Височината на кръглия вал на кратера може да определим, като измерим ширината на сянката, която той хвърля на дъното на кратера, и пресметнем ъгъла на падане на слънчевите лъчи.
На голямата снимка на Луната съединяваме върховете на лунния сърп с права линия и получаваме лунен диаметър. Измерваме дължината му и получаваме 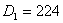 мм. Линейният диаметър на Луната е мм. Линейният диаметър на Луната е 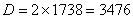 км. Следователно мащабът на снимката е 3476 / 224 ≈ 15.52 км на милиметър. Начертаваме през средата на кратера Коперник права линия, перпендикулярна на построения от нас диаметър. Измерваме дължината на отсечката до границата на лунния диск. Получаваме км. Следователно мащабът на снимката е 3476 / 224 ≈ 15.52 км на милиметър. Начертаваме през средата на кратера Коперник права линия, перпендикулярна на построения от нас диаметър. Измерваме дължината на отсечката до границата на лунния диск. Получаваме 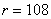 мм. По същата линия измерваме разстоянието a от диаметъра на лунния диск до терминатора и разстоянието b от диаметъра до вала на кратера, хвърлящ широката сянка. Получаваме мм. По същата линия измерваме разстоянието a от диаметъра на лунния диск до терминатора и разстоянието b от диаметъра до вала на кратера, хвърлящ широката сянка. Получаваме 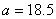 мм, мм, 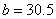 мм. мм.

Както се вижда от схемата по-долу, тези разстояния ни помагат да определим ъглите α , β и γ . На схемата с k е означено мястото на лунния кратер, или по-точно, на частта от вала на кратера, чиято височина искаме да узнаем.
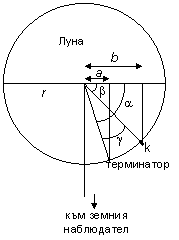
Последователно можем да пресметнем:
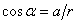 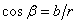
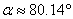 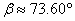
И накрая:
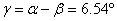
Следващата схема показва, че слънчевите лъчи падат по допирателни към лунната повърхност, там където е терминаторът. Равнината на хоризонта за мястото на кратера също е допирателна към лунната повърхност.
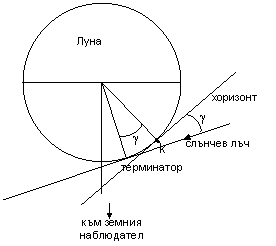
Така се убеждаваме, че ъгълът γ всъщност е равен на ъгъла, под който слънчевите лъчи падат към лунната повърхност около въпросния кратер, като ъгли с взаимно перпендикулярни рамене.
Вече ни остава само да определим ширината на сянката, която хвърля валът на кратера върху неговото дъно. За целта използваме увеличеното изображение. Измерваме ширината на сянката – тя е 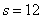 мм. Нека не забравяме, обаче, че участъкът от лунната повърхност, където е кратерът Коперник, не е перпендикулярен на лъча на зрение от нас към Луната. Той е под наклон към тази плоскост мм. Нека не забравяме, обаче, че участъкът от лунната повърхност, където е кратерът Коперник, не е перпендикулярен на лъча на зрение от нас към Луната. Той е под наклон към тази плоскост 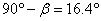 . Затова ние всъщност измерваме проекцията на сянката на вала. Истинската дължина на сянката ще бъде . Затова ние всъщност измерваме проекцията на сянката на вала. Истинската дължина на сянката ще бъде 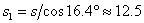 мм. Обаче, ако си представим вала на кратера като вертикална стена, ще се накланя и тя, като ще виждаме в проекция засенчената й страна. Това ще увеличава дължината на наблюдаваната сянка. Тъй като наклонът е малък, промяната на видимата дължина от двата ефекта е малък, като при това те действат в противоположни посоки. Това ни води до заключението, че може и да не отчитаме общата промяна, тъй като тя е в рамките на грешката, която допускаме при измерванията. мм. Обаче, ако си представим вала на кратера като вертикална стена, ще се накланя и тя, като ще виждаме в проекция засенчената й страна. Това ще увеличава дължината на наблюдаваната сянка. Тъй като наклонът е малък, промяната на видимата дължина от двата ефекта е малък, като при това те действат в противоположни посоки. Това ни води до заключението, че може и да не отчитаме общата промяна, тъй като тя е в рамките на грешката, която допускаме при измерванията.
Сега трябва да преминем към мащаба на голямата снимка. Сравняваме диаметъра в милиметри на кратера Коперник, измерен на увеличеното изображение – 40 мм, и диаметъра на същия кратер върху голямата снимка – 5.5 мм. Следователно, дължината на сянката върху голямата снимка трябва да бъде: 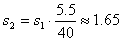 мм. Можем вече да превърнем тази величина в километри на лунната повърхност. Използваме получения в началото на решението мащаб и намираме: мм. Можем вече да превърнем тази величина в километри на лунната повърхност. Използваме получения в началото на решението мащаб и намираме:
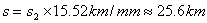
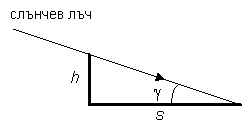
На схемата по-горе h е височината на вала, която търсим. Очевидно:
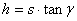
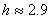 км км
|
|