МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА ПО АСТРОНОМИЯ
ХІІІ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
І кръг - задачи и решения
Ученици от 9-10 клас
1 задача. Съставяне на съзвездия.
• Двете животни, които виждате, наистина съществуват в природата. Едно от съзвездията изобразява митично същество, което се състои от части на тези животни. Кое е това съзвездие и от кои части на животните се състои митичното същество?
 
 • На снимката вляво виждате още едно истинско животно. Какво трябва да се добави към неговото тяло, за да се превърне в митичното същество, символ на поезията, което също присъства на небето като съзвездие? • На снимката вляво виждате още едно истинско животно. Какво трябва да се добави към неговото тяло, за да се превърне в митичното същество, символ на поезията, което също присъства на небето като съзвездие?
Решение:
Горните две животни са риба и рядко срещан вид див козел, наречен козирог. От тях може да се състави странното митично същество с глава на козел и опашка на риба. То е изобразено в съзвездието Козирог – едно от зодиакалните съзвездия.
Ако на коня поставим крила, той ще се превърне в митичния Пегас – крилатият кон, символ на летящата поетична мисъл и фантазия. Пегас също присъства на небето като съзвездие.

Козирог

Пегас
Критерии за оценяване:
За всяко подусловие по 4 т., от които за правилно “съставяне” на съзвездието от различните части на животни – 2т., за правилно посочване на името на съзвездието – 2 т.
2 задача. Фантастичен роман. Писател фантаст съчинява поредното си произведение. Ето докъде е стигнал и не знае как да продължи:
“С включването на най-мощните си двигатели звездолетът “Мечта” излезе от околоземна орбита и се понесе към своята далечна цел. Щурманът попита бордовия къмпютър:
І вариант. Приблизително колко път имаме до Орион?
ІІ вариант. Приблизително колко път имаме до Плеядите?”
• Ако вие бяхте бордовият компютър, който разбира малко повече от астрономия, кой вариант бихте посъветвали да избере писателят, за да има научна достоверност, и защо?
• Какво бихте отговорили на щурмана тогава?
Решение:
Съзвездията са възникнали като произволни фигури от звезди, в които с много въображение древните звездобройци са виждали разни легендарни герои и митични същества. Звездите от едно съзвездие могат да бъдат на много различни разстояния от нас. Те могат да са много отдалечени една от друга и по принцип да нямат нищо общо помежду си. Съзвездията не отразяват никакви реални физически връзки, обединяващи звездите. Освен това според съвременното определение съзвездието е област от небето, в която могат да се намират звезди и всякакви други космически обекти като планети, мъглявини и далечни галактики. Следователно въпросът колко път има до съзвездието Орион, е безмислен. Звездолетът не може да пътува до това съзвездие и да пристигне някога там, защото звездите от него не са в някаква обособена и ограничена от всички страни област от пространството.
Звездните купове, като Плеядите, са системи от звезди, които са разположени в ограничена област от пространството, сравнително близо една до друга. Те са реално свързани помежу си от гравитационното привличане и от общия си произход. Ето защо звездолетът наистина може да стигне до Плеядите. Писателят трябва да избере втория вариант.
От нас до Плеядите разстоянието е около 450 светлинни години. Това трябва да отговори бордовият компютър на въпроса на щурмана.
Критерии за оценяване:
За правилно обяснение по вариант І (Орион) – 3 т.
За правилно обяснение по вариант ІІ (Плеядите) – 3 т.
За крайния извод – верен избор на варианта, с който да продължи писателят – 1 т.
За намиране на информация за разстоянието до Плеядите – 1 т.
3 задача. Питагор. Древногръцкият учен и философ Питагор, живял през VІ век пр. н. е., е прочут не само с теоремата си за правоъгълния триъгълник. Той е доказвал кръглата форма на Земята с астрономически наблюдения. На снимката виждате явлението, което е наблюдавал.

• Какво е това явление?
• Представете си, че вие сте Питагор. Как ще докажете на събеседниците си своето твърдение?
• Направете измервания по снимката и определете приблизително колко пъти Земята е по-голяма от Луната.
Решение:
Явлението представлява частично лунно затъмнение. Лунното затъмнение се получава, когато Луната попадне в сянката, хвърляна от Земята. Съгласно аргументацията на Питагор, единственото тяло, което откъдето и да се освети, винаги хвърля кръгла сянка, е кълбото. Тъй като при лунно затъмнение земната сянка винаги е кръгла, следва да заключим, че Земята има форма на кълбо.
На снимката измерваме дължината на хордата A’A” от земната сянка:
A’A” = 2y = 60 mm.
Измерваме и отсечката МВ:
MB = x =20 mm. Означаваме центъра на земната сянка с О, а нейния радиус с r .
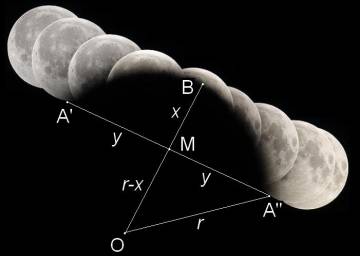
Разглеждаме триъгълника OA”M и като приложим към него теоремата на Питагор, получаваме:
OM2 + MA”2 = OA”2

От това уравнение намираме:
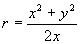
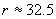 mm mm
Диаметърът на земната сянка ще бъде 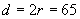 mm. Разбира се, има и различни други начини чрез други построения, по които можем да получим този диаметър. Остава да измерим диаметъра на изображението на Луната – mm. Разбира се, има и различни други начини чрез други построения, по които можем да получим този диаметър. Остава да измерим диаметъра на изображението на Луната – 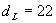 mm. Сравняваме диаметъра на земната сянка и диаметъра на Луната: mm. Сравняваме диаметъра на земната сянка и диаметъра на Луната: 
Можем да приемем, че истинският земен диаметър е толкова пъти по-голям от диаметъра на Луната, колкото диаметърът на земната сянка е по-голям от лунния диаметър. Така заключаваме, че Земята е около 3 пъти по-голяма от Луната.
В действителност конусът на земната сянка се стеснява с отдалечаване от Земята и съотношението на истинските размери на двете тела е по-голямо от полученото. Диаметърът на Земята е 12756 km, а на Луната 3476 km. Истинското съотношение на размерите е  . (Забележка: Това разсъждение не се изисква в решението на задачата. Ако някой участник е направил самостоятелно подобно сравнение, следва да му се присъждат допълнителни точки за награда). . (Забележка: Това разсъждение не се изисква в решението на задачата. Ако някой участник е направил самостоятелно подобно сравнение, следва да му се присъждат допълнителни точки за награда).
Критерии за оценяване:
За правилно определяне на явлението като частично лунно затъмнение – 2 т.
За обосновката за кръглата форма на Земята – 2 т.
За правилни построения и математическо решение на третото подусловие – 3 т.
За верен числен отговор – 1 т.
4 задача. Телескоп. Потърсете информация за най-големия телескоп в България.
• Къде се намира той?
• Какъв е диаметърът на неговия обектив?
• Когато наблюдаваме с телескоп, ние все едно гледаме с гигантско око, чиято зеница е голяма колкото обектива на телескопа и събира много повече светлина от нашето око. Пресметнете приблизително колко пъти по-слаби звезди можем да видим, ако погледнем през този телескоп, отколкото най-слабите звезди, които виждаме с невъоръжено око. Считайте, че при адаптация към тъмнината зеницата на окото има диаметър около 6 мм. (Забележка: Получената по този начин оценка е много приблизителна и в нея не са отразени редица важни фактори, които влияят на т.нар. проникваща способност на телескопа.)
• Оценете колко пъти по-далечни обекти бихме видели през телескопа, в сравнение с онези, които виждаме с просто око.
Решение:
Най-големият телескоп в България се намира в Националната астрономическа обсерватория в местността Рожен, в Родопите. Диаметърът на неговия обектив е 2 метра.
Блясъкът на звездите, който възприемаме с очите си, зависи от количеството светлина, попадащо в нашите зеници. Нека си представим, че виждаме една звезда отначало с невъоръжено око. Да предположим, че след това наблюдаваме същата звезда с двуметровия телескоп с подходящ окуляр, така че цялата събрана от неговия обектив светлина да попада в зеницата на окото ни. Така ние ще възприемаме звездата толкова пъти по-ярка, отколкото при гледане с просто око, колкото пъти площта на обектива на телескопа е по-голяма от площта на нашата зеница. Като имаме предвид, че площта на кръг с диаметър d е  , получаваме: , получаваме:
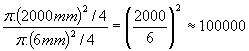
При гледане през двуметровия телескоп бихме могли да видим около 100 000 пъти по-слаби звезди от най-слабите, които виждаме с просто око.
Осветеността, която един космически обект създава на определено разстояние, е обратно пропорционална на квадрата на това разстояние. Следователно при наблюдение през двуметровия телескоп бихме могли да видим обекти, които са на  пъти по-големи разстояния, отколкото най-далечните обекти, видими с просто око (при еднаква светимост на обектите). Най-далечният обект, видим с просто око, е галактиката Андромеда, означавана от астрономите с М31. Тя се намира на около 2 000 000 светлинни години. Теоретично, през двуметровия телескоп бихме могли да видим галактики, подобни на М31, които са на разстояние около 600 000 000 светлинни години. пъти по-големи разстояния, отколкото най-далечните обекти, видими с просто око (при еднаква светимост на обектите). Най-далечният обект, видим с просто око, е галактиката Андромеда, означавана от астрономите с М31. Тя се намира на около 2 000 000 светлинни години. Теоретично, през двуметровия телескоп бихме могли да видим галактики, подобни на М31, които са на разстояние около 600 000 000 светлинни години.
В интерес на точността следва да се отбележи, че астрономите днес практически не наблюдават със собствените си очи през телескопа. Те използват други, много по-чувствителни устройства за получаване на изображения на космическите обекти, при които светлинното въздействие може да се натрупва за дълго време. По този начин могат да се изследват още по-слаби източници на светлина. Освен това много от далечните галактики и особено квазарите са значително по-ярки от галактиката Андромеда и на практика най-далечните обекти, наблюдавани с двуметровия телескоп в Националната астрономическа обсерватория, са на разстояния, значително по-големи от 600 милиона светлинни години. (Забележка: Тези разсъждения не се изискват от учениците при решаването на задачата. Ако накой участник е привел подобни съображения, следва да получи допълнителни точки за награда).
Критерии за оценяване:
За първото и второто подусловия – общо 2 т.
За правилни разсъждения и математическо решение на третото подусловие – 3 т., за верен числен отговор – 1 т.
За четвъртото подусловие – 2 т. (Забележка: Примерът с галактиката Андромеда не се изисква в решението на задачата).
5 задача. Спътници на Юпитер. Спътниците на Юпитер Йо и Европа имат периоди на околоосно въртене, съвпадащи с орбиталните им периоди на движение около Юпитер. Затова всеки от тези спътници е винаги обърнат към Юпитер с една и съща своя страна, както Луната към Земята. Орбиталните периоди на Йо и Европа са съответно 42.5 часа и 85 часа. Радиусите на техните орбити са 420 000 и 670 000 км.
• Вие участвате в експедиция за изследване на вулканите на Йо и корабът ви е кацнал в центъра на обратната страна на спътника, т.е. тази, която не е обърната към Юпитер. През какъв период от време ще виждате Европа да преминава през зенита? Йо и Европа обикалят около Юпитер в една и съща посока.
• Начертайте схема в подходящ мащаб на орбитите на Йо и Европа около Юпитер. Отбележете приблизително положенията на Европа спрямо Йо в моментите, когато от вашия кораб виждате Европа при изгрев, в зенита и при залез.
• Направете по схемата измерване на необходимия ъгъл с транспортир и определете приблизително колко време след изгрева Европа преминава през зенита за вас.
Решение:
Забелязваме, че периодът на обикаляне на Европа около Юпитер е два пъти по-дълъг от този на Йо. Начертаваме в подходящ мащаб орбитите на Йо и Европа около Юпитер.
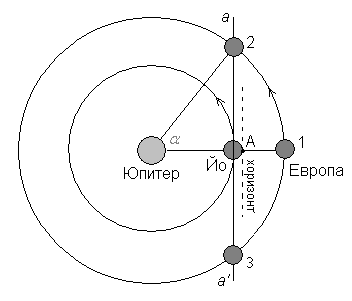
Отбелязваме с точка А върху спътника Йо местоположението на нашия кораб. Нека в даден момент оттам ние да виждаме Европа в зенита. Тогава този спътник трябва да е в положение 1. След една обиколко около Юпитер на Йо, Европа ще е направила половин обиколка. Двете тела ще застанат пак така, че от Йо да виждаме Европа в зенита след още една обиколка на Йо около Юпитер. Следователно периодът, през който ще виждаме Европа в зенита, ще е равен на два орбитални периода на Йо, или един орбитален период на Европа, т.е. 85 часа.
Това лесно може да се получи и от съотношението между орбиталните периоди на Йо и Европа – T’ и T” , и синодичния период на Европа за наблюдател на Йо – TS :

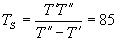 ч. ч.
Европа има по-дълъг орбитален период от Йо – тя непрекъснато изостава от него при движението си около Юпитер. Нека преминем в координатна система, в която Йо е неподвижен. Относно тази система Европа ще се движи в посока обратна на истинската посока на движение на спътниците с период, равен на своя синодичен период спрямо Йо, или 85 часа. С пунктирана линия сме начертали хоризонта за наблюдател в точка А на Йо. Но тъй като радиусът на Йо е много по-малък от радиусите на орбитите на двата спътника, то можем да го пренебрегнем и за по-просто да начертаем хоризонта през центъра на спътника – линията аа’ . За да виждаме Европа на хоризонта при изгрев, този спътник трябва да е в положение 2. Известно време след това Европа ще се придвижи за нас в положение 1 и ще бъде в зенита. При залеза си Европа ще бъде в положение 3.
Измерваме ъгъла a , който се оказва около 51°. Времето, което ще измине от изгрева на Европа до преминаването й през зенита, ще бъде:
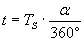
 часа часа
Критерии за оценяване:
За правилно обяснение и пресмятане на периода между две преминавания на Европа през зените – 3 т.
За верен чертеж на положенията на Европа при изгрев, в зенита и при залез – 2 т.
За вярно пресмятане на периода от изгрева до появата в зенита на Европа – 3 т.
6 задача. Древна астрономия.
 Тази рисунка е издялана върху камък преди много хиляди години. На нея първобитният човек търпеливо и последователно, ден след ден е отразявал нещо, което е наблюдавал на небето. Фигурките са направени неточно и непохватно, времето също е повлияло върху тях. Но те изобразяват повтаращи се явления, които можем да разпознаем и днес. Какво представлява рисунката? Обосновете подробно вашето предположение. Тази рисунка е издялана върху камък преди много хиляди години. На нея първобитният човек търпеливо и последователно, ден след ден е отразявал нещо, което е наблюдавал на небето. Фигурките са направени неточно и непохватно, времето също е повлияло върху тях. Но те изобразяват повтаращи се явления, които можем да разпознаем и днес. Какво представлява рисунката? Обосновете подробно вашето предположение.
Решение:
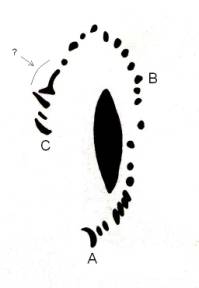 На камъка са изобразени лунните фази за всеки ден в рамките на един синодичен месец. Ако предположим, че авторът на рисунката е обитавал северното полукълбо, то сърпът, обърнат с изпъкналата си страна надясно и означен с А, съответства на младата Луна – фаза около един ден след новолуние. В следвашите дни астрономът от първобитната епоха е отразявал ежедневно промяната на вида на Луната, докато се стигне до пълнолунието, означено с В на рисунката. Накрая старата Луна, означена с С, е изглеждала като тънък сърп, обърнат с изпъкналата си страна наляво. В следващите 1-2 дни Луната не се е виждала, което съответства на празното място между С и А, и после започва новият цикъл на лунните фази. На камъка са изобразени лунните фази за всеки ден в рамките на един синодичен месец. Ако предположим, че авторът на рисунката е обитавал северното полукълбо, то сърпът, обърнат с изпъкналата си страна надясно и означен с А, съответства на младата Луна – фаза около един ден след новолуние. В следвашите дни астрономът от първобитната епоха е отразявал ежедневно промяната на вида на Луната, докато се стигне до пълнолунието, означено с В на рисунката. Накрая старата Луна, означена с С, е изглеждала като тънък сърп, обърнат с изпъкналата си страна наляво. В следващите 1-2 дни Луната не се е виждала, което съответства на празното място между С и А, и после започва новият цикъл на лунните фази.
Лунните фази се сменят с период един синодичен месец, който се равнява приблизително на 29.5 денонощия. Не е съвсем ясно колко последователни лунни фази са отбелязани на камъка. Бихме могли да приемем, че означеното със стрелка изображение представлява всъщност две изображения, които изглеждат слети поради някаква пукнатина или друга случайна следа върху камъка. Тогава можем да считаме, че на камъка са отбелязани 27 последователни лунни фази. Липсващите още две съответстват на интервала от време около новолунието, когато Луната не се наблюдава.
Критерии за оценяване:
За правилен отговор на въпроса – 2 т.
За правилно посочване на последователността на смяната на фазите и техните названия – 3 т.
За разсъждения относно броя на лунните изображения и дните в синодичния месец – 3 т.
|