МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА ПО АСТРОНОМИЯ
ХІІІ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
І кръг - задачи и решения
Ученици от 11-12 клас
1 задача. Знаменити астрономи.
• Кой е астрономът, открил планетарните мъглявини, инфрачервените лъчи, конструирал телескопи и изследвал структурата на Млечния път? Какво е най-забележителното му откритие в астрономията?
• Кой астроном след дългогодишно изследване на движението на Марс е открил, че тази планета се движи не по окръжност, както дотогава се е смятало, а по елипса? Какъв е най-големият му теоретичен принос в астрономията?
• Кой астроном за първи път е предсказал появата на комета, използвайки теорията на Нютон за всемирното привличане?
• Кой астроном е открил важен елемент от структурата на пръстените на Сатурн, голямото червено петно на Юпитер, а също и за първи път определя разстоянието до Марс? Какво е предназначението на космическата станция, наречена на негово име?
• Посочете за всеки астроном кой е неговият портрет.
Решение:
Планетарните мъглявини и инфрачервените лъчи са открити от знаменития английски астроном от немски произход Уилям Хершел. Той има забележителен принос в много области на астрономията, но най-знаменателното е, че е открил планетата Уран.
Елиптичната форма на орбитата на Марс е била открита от немския астроном Йохан Кеплер. Най-големият му теоретичен принос в астрономията е формулирането на трите закона за движението на планетите около Слънцето, известни днес като закони на Кеплер. С тях той е уточнил и усъвршенствал хелиоцентричната система на Николай Коперник.
За първи път появата на комета е била предсказана от английския астроном Едмънд Халей. Използвайки теорията на Нютон, той е разработил метод за определянето на орбитите на телата в Слънчевата система. Така Халей е открил, че някои от историческите наблюдения на комети са свързани не с появата на различни комети, а с многократни появявания на една и съща комета, обикаляща около Слънцето с период 76 години. Тази комета днес наричаме Халеевата комета.
Важният елемент от структурата на пръстените на Сатурн е т.нар. процеп на Касини – зона от пръстените, бедна на частици, поради което изглежда тъмна. Той е открит от италианския астроном Джовани Касини. Станцията Касини се движи в орбита около Сатурн и изследва планетата, нейните пръстени и спътници. През 2005 г. от станцията се отдели сондата Хюйгенс, която кацна на най-големия спътник на Сатурн Титан.
   
Едмънд Халей Джовани Касини Уилям Хершел Йохан Кеплер
Критерии за оценяване:
За Уилям Хершел и най-важното му откритие – 1.5 т.
За Кеплер и теоретичния му принос в астрономията – 1.5 т.
За Халей – 1 т.
За Касини, процепа на Касини и станцията Касини – 2 т.
За свързването на имената с портретите – 2 т.
2 задача. Сатурн. Пръстените на Сатурн са наклонени спрямо орбиталната му равнина около Слънцето. При движението на Сатурн около Слънцето ние виждаме пръстените по различен начин в различни моменти от време, а понякога те са почти невидими, защото застават ребром спрямо нас. Горната снимка е направена от космическия телескоп Хъбъл, когато това се е случило за последен път през ХХ век. Долната снимка е направена от същия телескоп на 7 март 2003 г., когато наклонът на пръстените спрямо зрителния лъч от нас към планетата е бил максимален.


• В коя година приблизително е направена горната снимка? Обяснете вашия отговор.
• Направете необходимите измервания и определете под какъв ъгъл спрямо зрителния лъч са наклонени пръстените на Сатурн на долната снимка.
• С колко километра най-близката до нас точка от пръстените на Сатурн е по-близо, отколкото най-далечната точка от пръстените на долната снимка?.
Решение:
Периодът на обикаляне на Сатурн около Слънцето е приблизително 30 години. При орбиталното движение на планетата равнината на пръстените остава успоредна сама на себе си (ако не отчитаме известни малки смущения, предизвикани от гравитационното въздействие на спътниците). Радиусът на орбитата на Сатурн е около 9.5 пъти по-голям от радиуса на земната орбита. Можем да приемем, че поради малкия радиус на земната орбита, от позицията на Земята ние наблюдаваме Сатурн приблизително така, както бихме го виждали от самото Слънце. За един 30-годишен период ще наблюдаваме два пъти пръстените ориентирани ребром към нас, както на лявата снимка – т.е. през 15 години (положения 1 и 3 на схемата), и два пъти с максимален наклон към зрителния лъч (положения 2 и 4 на схемата).

Следователно от момента, регистриран на горната снимка, до март 2003 г. трябва да е изминал период от време около 30/4 =7.5 години. Горната снимка вероятно е направена през 1995 г. Така се оказва и в действителност – снимката е от август 1995 г. На практика тези характерни изгледи на пръстените на Сатурн – ребром и под максимален ъгъл – не се редуват точно през 7.5 години поради неравномерното движение на Сатурн по неговата елиптична орбита и поради това, че все пак го наблюдаваме от Земята, която може да се намира на различни места по своята орбита спрямо Сатурн и Слънцето.
На долната снимка пръстените на Сатурн изглеждат като елипса. Измерваме голямата и малката ос на тази елипса и получаваме съответно:
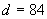 mm mm  mm mm
На схемата по-долу е показано как ние виждаме Сатурн. С D и D’ са означени истинският диаметър на пръстените и по-малкият размер на тяхната проекция, съответстващ на малката ос на елипсата, която виждаме.

Очевидно е в сила съотношението:

където a е търсеният от нас ъгъл. Оттук намираме:
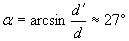
Разстоянията от нас до най-близката и най-далечната точка от пръстените на Сатурн се различават с величина, равна на дължината на отсечката х на схемата. Лесно се вижда, че 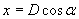 . Диаметърът на пръстените на Сатурн е около 280 000 km. Оттук пресмятаме: . Диаметърът на пръстените на Сатурн е около 280 000 km. Оттук пресмятаме: 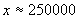 km. km.
Критерии за оценяване:
За правилни разсъждения по въпроса в коя година е направена лявата снимка – 2 т., за вярно определяне на годината – 1 т.
За правилна геометрична и математическа постановка на решението на второто подусловие – 2 т. За верен числен отговор – 1 т.
За третото подусловие – 2 т.
3 задача. Питагор. Древногръцкият учен и философ Питагор, живял през VІ век пр. н. е., е прочут не само с теоремата си за правоъгълния триъгълник. Той е доказвал кръглата форма на Земята с астрономически наблюдения. На снимката виждате явлението, което е наблюдавал.

• Какво е това явление?
• Представете си, че вие сте Питагор. Как ще докажете на събеседниците си своето твърдение?
• Направете измервания по снимката и определете приблизително колко пъти Земята е по-голяма от Луната.
• Сравнете вашата оценка с истинското съотношение на диаметрите на Земята и Луната. Обяснете защо има разлика.
Решение:
Явлението представлява частично лунно затъмнение. Лунното затъмнение се получава, когато Луната попадне в сянката, хвърляна от Земята. Съгласно аргументацията на Питагор, единственото тяло, което откъдето и да се освети, винаги хвърля кръгла сянка, е кълбото. Тъй като при лунно затъмнение земната сянка винаги е кръгла, следва да заключим, че Земята има форма на кълбо.
На снимката измерваме дължината на хордата A’A” от земната сянка:
A’A” = 2y = 60 mm.
Измерваме и отсечката МВ:
MB = x =20 mm. Означаваме центъра на земната сянка с О, а нейния радиус с r .
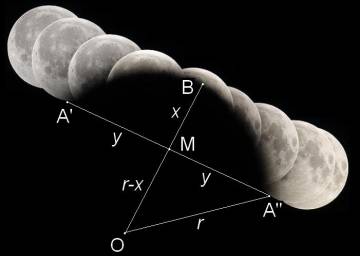
Разглеждаме триъгълника OA”M и като приложим към него теоремата на Питагор, получаваме:
OM2 + MA”2 = OA”2

От това уравнение намираме:
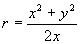
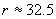 mm mm
Диаметърът на земната сянка ще бъде 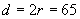 mm. Разбира се, има и различни други начини чрез други построения, по които можем да получим този диаметър. Остава да измерим диаметъра на изображението на Луната – mm. Разбира се, има и различни други начини чрез други построения, по които можем да получим този диаметър. Остава да измерим диаметъра на изображението на Луната – 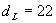 mm. Сравняваме диаметъра на земната сянка и диаметъра на Луната: mm. Сравняваме диаметъра на земната сянка и диаметъра на Луната: 
Можем да приемем, че истинският земен диаметър е толкова пъти по-голям от диаметъра на Луната, колкото диаметърът на земната сянка е по-голям от лунния диаметър. Така заключаваме, че Земята е около 3 пъти по-голяма от Луната.
В действителност конусът на земната сянка се стеснява с отдалечаване от Земята и съотношението на истинските размери на двете тела е по-голямо от полученото. Диаметърът на Земята е 12756 km, а на Луната 3476 km. Истинското съотношение на размерите е  . .
Критерии за оценяване:
За правилно определяне на явлението като частично лунно затъмнение – 1 т.
За обосновката за кръглата форма на Земята – 2 т.
За правилни построения и математическо решение на третото подусловие – 2 т.
За верен числен отговор – 1 т.
За намиране на информация за истинските размери на Земята и Луната и определяне на съотношението им – 1 т.
За правилно обяснение защо това отношение е различно от полученото – 1 т.
4 задача. Плутон-експрес. Вие сте специалист по ледените гейзери и пътувате в междупланетния кораб “Плутон-експрес” към планетата джудже Плутон. Там вашият екипаж ще смени колегите ви, които са работили вече дълго време. “Плутон-експрес” е изведен в околоземното космическо пространство. Стартират йонните му двигатели и създават тяга, която задвижва кораба с постоянно ускорение, равно на земното ускорение. На борда му вие се чувствате както при нормалната земна гравитация.
• Как трябва да протече полетът, за да може екипажът да се чувства така комфортно почти през цялото време, корабът благополучно да стигне до Плутон и да се извърши смяната на изследователите?
• Каква ще бъде максималната скорост, която ще достигне “Плутон-експрес”?
• За колко време корабът ще стигне до Плутон?
Решение:
Ако корабът се движи с постоянно ускорение по време на целия полет, то при достигането до Плутон той ще е набрал значителна скорост и ще бъде трудно да кацне на планетата или да влезе в орбита около нея. За да се чувстват максимално комфортно космонавтите през по-голямата част от времето на полета, по-добре е той да се движи с постоянно ускорение до средата на разстоянието от Земята до Плутон. После двигателите трябва за кратко да се изключат, корабът да се обърне на 180°, така че носът му да сочи противоположно на крайната цел, и двигателите отново да се включат. Така корабът ще измине втората половина от разстоянието в режим на равнозакъснително движение. Ускорението му ще бъде отрицателно, но равно по големина на земното ускорение, така че екипажът отново ще има същото усещане за нормално тегло. Освен това при достигане до планетата скоростта на кораба ще е намалена до стойност, при която ще могат лесно да се извършат маневрите за влизане в орбита или кацане на планетата.
За да пресметнем максималната скорост, която ще има корабът по време на пътешествието, и времетраенето на полета, по принцип трябва да знаем каква е началната скорост на кораба и по каква траектория се движи той. Йонните двигатели стартират, когато корабът е в близките околности на Земята, но в условието не е уточнено къде е той и каква е началната му скорост, а също и къде е самата Земя по своята орбита и къде е Плутон. Плутон се движи по елиптична орбита с доста голям ексцентрицитет, но за да направим приблизително пресмятане, ще считаме, че се намира на средното си разстояние от Слънцето. То е 39.5 астрономически единици, или 39.5 пъти по-голямо, отколкото разстоянието от Земята до Слънцето. Виждаме, че за приблизителната ни оценка няма особено значение къде точно се намира Земята по орбитата си в момента на тръгването на кораба към Плутон.
Каква е началната скорост на кораба? Орбиталната скорост на Земята около Слънцето е около 30 km/s. След извеждането в околностите на Земята, скоростта на кораба относно Слънцето трябва да е приблизително такава. Със стартирането на йонните двигатели корабът започва да се движи с ускорение, равно на земното ускорение:
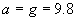 m/s2 m/s2
С такова ускорение скорост, равна на орбиталната скорост на Земята, се достига за по-малко от един час. А корабът ще пътува много по-дълго и през повечето от времето на полета към Плутон ще се движи с много по-голяма скорост от тази. Следователно можем въобще да не отчитаме началната скорост на кораба, т.е да я смятаме за равна на нула.
По каква траектория ще се движи корабът? За да разсъждаваме върху това, трябва да разгледаме въпроса за гравитационното влияние на Слънцето върху кораба. В околностите на Земята Слънцето придава на кораба ускорение:

където  m3/kg.s2 е гравитационната константа, m3/kg.s2 е гравитационната константа, 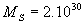 kg е масата на Слънцето, kg е масата на Слънцето, 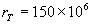 km е разстоянието Земя – Слънце. Като заместим тези стойности, получаваме: km е разстоянието Земя – Слънце. Като заместим тези стойности, получаваме:
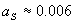 m/s2 m/s2
Очевидно 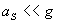 и в сравнение с реактивната тяга на двигателите, въздействието на Слънцето върху кораба е пренебрежимо малко. Можем изобщо да не го отчитаме. Така че корабът може да се движи праволинейно – равноускорително с ускорение g от Земята до средата на пътя и равнозакъснително с ускорение –g оттам нататък до Плутон. Тъй като разстоянието Земя – Слънце е много по-малко от разстоянието Слънце – Плутон, и понеже не знаем къде е Земята по орбитата си в момента на тръгването, то приемаме, че до Плутон корабът има да изминава по права линия път: и в сравнение с реактивната тяга на двигателите, въздействието на Слънцето върху кораба е пренебрежимо малко. Можем изобщо да не го отчитаме. Така че корабът може да се движи праволинейно – равноускорително с ускорение g от Земята до средата на пътя и равнозакъснително с ускорение –g оттам нататък до Плутон. Тъй като разстоянието Земя – Слънце е много по-малко от разстоянието Слънце – Плутон, и понеже не знаем къде е Земята по орбитата си в момента на тръгването, то приемаме, че до Плутон корабът има да изминава по права линия път:
 km km
Означаваме с t времето, за което коръбът ще измине половината от това разстояние. Можем да напишем:

Оттук получаваме:
 денонощия денонощия
По средата на полета корабът се обръща в противоположна посока и се движи равнозакъснително със същото ускорение. Лесно се съобразява, че общото време на полета ще бъде:  денонощия. денонощия.
Корабът ще има максимална скорост точно по средата на пътя. Тя ще бъде:
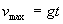
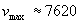 km/s km/s
Това ни показва, че корабът ще достигне до много висока скорост, на порядъци превишаваща скоростите, с които се движат космическите апарати понастоящем. Но тя все пак ще бъде много по-малка от скоростта на светлината, поради което при решаването на задачата не е необходимо използването на формули от специалната теория на относителността.
Критерии за оценяване:
За правилен отговор на първото подусловие – 2 т.
За разсъждения и приети приблизителни допускания относно началната скорост и траекторията на кораба – 2 т.
За пресмятане на максималната скорост – 2 т.
За пресмятане на времето на полета – 2 т.
Забележка: Участникът в олимпиадата може да е решил задачата при предположение, че през цялото време корабът се движи равноускорително. Пресмятанията при това условие ще доведат до други числени стойности за времето на полета и максималната скорост (която тогава ще се получи в края на полета при достигането до Плутон):
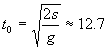 денонощия, денонощия, 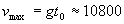 km/s km/s
В такива случаи следва да се отнемат 2 точки от оценката за неправилното планиране на полета, но ако пресмятанията са верни, да се дават пълните точки за другите подусловия.
5 задача. Спътници на Юпитер. Спътниците на Юпитер Йо и Европа имат периоди на околоосно въртене, съвпадащи с орбиталните им периоди на движение около Юпитер. Затова всеки от тези спътници е винаги обърнат към Юпитер с една и съща своя страна, както Луната към Земята. Орбиталните периоди на Йо и Европа са съответно 42.5 часа и 85 часа. Радиусите на техните орбити са 420 000 и 670 000 км.
• Вие участвате в експедиция за изследване на вулканите на Йо и корабът ви е кацнал в центъра на обратната страна на спътника, т.е. тази, която не е обърната към Юпитер. През какъв период от време ще виждате Европа да преминава през зенита? Йо и Европа обикалят около Юпитер в една и съща посока.
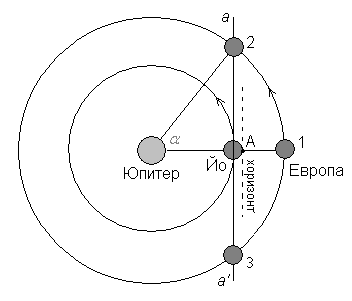
• Нарисувайте схема на орбитите на Йо и Европа около Юпитер. Отбележете приблизително положенията на Европа спрямо Йо в моментите, когато от вашия кораб виждате Европа при изгрев, в зенита и при залез.
• Пресметнете приблизително колко време след изгрева Европа преминава през зенита за вас.
Решение:
Забелязваме, че периодът на обикаляне на Европа около Юпитер е два пъти по-дълъг от този на Йо. С точка А върху спътника Йо на схемата е отбелязано положението на нашия кораб. Нека в даден момент оттам ние да виждаме Европа в зенита. Тогава този спътник трябва да е в положение 1. След една обиколко около Юпитер на Йо, Европа ще е направила половин обиколка. Двете тела ще застанат пак така, че от Йо да виждаме Европа в зенита след още една обиколка на Йо около Юпитер. Следователно периодът, през който ще виждаме Европа в зенита, ще е равен на два орбитални периода на Йо, или един орбитален период на Европа, т.е. 85 часа.
Това лесно може да се получи и от съотношението между орбиталните периоди на Йо и Европа – T’ и T” , и синодичния период на Европа за наблюдател на Йо – TS :
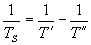
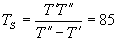 ч. ч.
Европа има по-дълъг орбитален период от Йо – тя непрекъснато изостава от него при движението си около Юпитер. Нека преминем в координатна система, в която Йо е неподвижен. Относно тази система Европа ще се движи в посока обратна на истинската посока на движение на спътниците с период, равен на своя синодичен период спрямо Йо, или 85 часа. С пунктирана линия сме начертали хоризонта за наблюдател в точка А на Йо. Но тъй като радиусът на Йо е много по-малък от радиусите на орбитите на двата спътника, то можем да го пренебрегнем и за по-просто да начертаем хоризонта през центъра на спътника – линията аа’ . За да виждаме Европа на хоризонта при изгрев, този спътник трябва да е в положение 2. Известно време след това Европа ще се придвижи за нас в положение 1 и ще бъде в зенита. При залеза си Европа ще бъде в положение 3.
За ъгъла a можем да напишем:
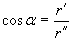
където r’ и r” са радиусите на орбитите на Йо и Европа.
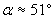
Времето, което ще измине от изгрева на Европа до преминаването й през зенита, ще бъде:
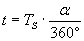
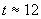 часа часа
Критерии за оценяване:
За правилно обяснение и пресмятане на периода между две преминавания на Европа през зените – 3 т.
За верен чертеж на положенията на Европа при изгрев, в зенита и при залез – 2 т.
За вярно пресмятане на периода от изгрева до появата в зенита на Европа – 3 т.
6 задача. Екзопланети. В последно време с усъвършенстването на наблюдателната техника, се откриват множество планети около други звезди. Най-вълнуващият въпрос, свързан с това изследване, е дали и кога ще открием някоя планета, подобна на нашата и може би населена с живот. За съжаление, обаче, огромното множество от планети около други звезди, които откриваме, са много различни от Земята и, меко казано, странни. Те са с много големи маси, сравними с масата на Юпитер, като същевременно са необикновено близо до своите звезди, често пъти по-близо, отколкото е Меркурий до Слънцето.
Защо засега успяваме да открием предимно такива планети?
Решение:
Планети около други звезди се откриват главно по косвени методи. С много малки изключения планетите около други звезди не могат да се наблюдават пряко. Два от най-често използваните методи се основават на гравитационното въздействие на планетата върху звездата. Звездата и планетата обикалят около общия си център на масите. Движението на звездата около този център се наслагва върху движението й през междузвездното пространство. Поради това при наблюдение на собственото движение на звездата на фона на другите звезди се откриват отклонения от плавната траектория, или по-точно – траекторията на звездата през междузвездното пространство изглежда вълнообразна. Ако орбиталната равнина на планетата и звездата сключва малък ъгъл със зрителния лъч на земния наблюдател, то при спектрални изследвания се вижда периодично отместване на спектралните линии на звездата ту към дълговълния, ту към късовълновия край на спектъра. То се обяснява с ефекта на Доплер и се дължи на това, че в различни моменти от времето звездата се движи около центъра на масите ту в посока от нас, ту към нас. Оклоненията, наблюдавани по тези два метода, позволяват да се открие присъствието на планети около съответните звезди и да се определят някои параметри на планетите и техните орбити. Но тези отклонения са много малки поради незначителните маси на планетите в сравнение със звездите. Ето защо се откриват предимно много масивни планети, намиращи се на необикновено близки разстояния до своите звезди, така че да предизвикват по-големи отклонения в тяхното движение. Това обаче, съвсем не означава, че болшинството от действително съществуващите планети са такива.
Друг широко използван метод за откриване на планети около други звезди е наблюдаване на т.нар. пасажи или преминавания на планетите пред звездите. Всъщност това, което се регистрира, е леко понижение на блясъка на дадена звезда за определено време. От получената крива на изменение на блясъка на звездата се съди за размерите на преминаващата пред нея планета. Изменението на блясъка е с изключително малка величина. Затова и по този метод могат да се откриват само достатъчно големи по размери планети, предизвикващи понижение на блясъка на звездите, което да може да се измери. Освен това, разстоянието от планетата, откривана по този начин, до звездата пак трябва да е малко. С увеличаване на разстоянието от планетата до звездата вероятността земният наблюдател да се намира в зоната, откъдето могат да се наблюдават пасажи на планетата на фона на звездата, намалява. Също така малкият радиус на планетната орбита предполага кратък орбитален период около звездата, а това позволява многократно наблюдение на пасаж, чрез което се потвърждава откриването на планетата и се уточняват найните параметри.
Критерии за оценяване:
За описание и обяснение на методите за откриване на планети около други звезди – 4 т.
За обоснован отговор на въпроса – 4 т.
|