|
МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО
И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА
ПО АСТРОНОМИЯ
ХIІІ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
http://astro-olymp.org
ІV кръг, теоретичен тур - решения
Ученици младша възраст (до 16 г.)
1 задача. „Претегляне” на Слънцето. Астрономите любители Калин Кръстев и Ивайло Полихронов са получили от своя ръководител странната задача да „претеглят” Слънцето с помощта на спектрограф. Използвайки знанията си от астрономическата олимпиада, те решават да направят спектрални наблюдения на звездата Алдебаран. Оказва се, че лъчевата й скорост се променя между +24 км/с и +84 км/с с период една година.
• Приблизително кога през годината лъчевата скорост на звездата е максимална и кога – минимална? Обяснете вашия отговор.
• Като използвате само тези данни, определете разстоянието от Земята до Слънцето.
• Как астрономите любители са определили масата на Слънцето? Направете го и вие.
Решение:
Промяната на лъчевата скорост на Алдебаран спрямо земния наблюдател се дължи на орбиталното движение на Земята около Слънцето. Понеже във всеки един момент скоростта на планетата ни е насочена в различно направление, то постоянно се изменя и лъчевата скорост на всяка звезда, включително и на Алдебаран, относно земния наблюдател. Земята обикаля около Слънцето с период един година, поради което и лъчевата скорост на звездите спрямо нея се изменя с такъв период.
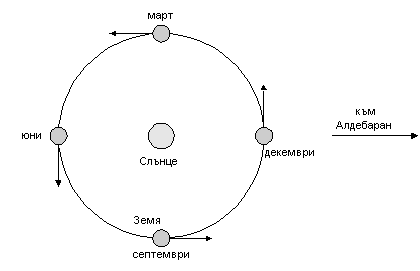
Звездата Алдебаран е разположена в зодиакалното съзвездие Бик. Можем да приемем, че е близо до еклиптиката, т.е. намира се почти в равнината, в която се осъществява движението на Земята около Слънцето. Следователно има периоди в година, през които планетата ни се приближава или отдалечава директно към или от тази звезда. В първия случай лъчевата скорост на Алдебаран е минимална, а във втория е максимална. Сънцето е в съзвездието Бик през юни. Т.е. звездата е в опозиция спрямо Слънцето през декември. Земята се приближава директно към нея 3 месеца преди опозицията й, или през септември. Тогава е и моментът на минимална лъчева скорост на Алдебаран. Аналогично, моментът, в който планетата ни се отдалечава най-бързо от звездата, или моментът, в който лъчевата скорост е максимална, е три месеца след опозицията – през март.
Самата звезда се движи в Галактиката и има собствена лъчева скорост спрямо Слънцето. Ако означим с V0 лъчевата скорост на Алдебаран за наблюдател на Слънцето, а с VЗ орбиталната скорост на Земята, то дадените ни минимална и максимална лъчева скорост на звездата са съответно:
Vmin = V0 – VЗ Vmax = V0 + VЗ.
Оттук следва, че:
VЗ = (Vmax – Vmin) / 2 = 30 km/s
Орбиталният период на Земята е Т = 1 година, следователно радиусът на орбитата й е:
r = VЗТ / 2? ≈ 150 млн. км
Понеже считаме земната орбита за кръгова, то скоростта на Земята по нея е равна на кръговата скорост за това разстояние от Слънцето. Ако M0 е масата на Слънцето, то:

където γ е гравитационната константа. По-нататък намираме:
М0 = VЗ2 r / γ
M0 ≈ 2×1030 kg.
2 задача. Комета на хоризонта. През 2020 г. младият астроном Десислава Жекова открива нова комета с орбита, лежаща в равнината на еклиптиката. На 30 септември сутринта тя наблюдава кометата, намираща се на малко ъглово разстояние от Слънцето. Наблюденията се провеждат в Астрономическата обсерватория на град Русе с координати φ = 43°50′, λ = 25°58′.
• Намерете ъгъла, който кометната опашка сключва с хоризонта. Не отчитайте рефракцията.
• Нарисувайте схема на хоризонта и ориентацията на кометната опашка с посоките на света.
• Отговорете качествено как рефракцията ще повлияе на ориентацията и формата на кометната опашка, ако главата на кометата е на хоризонта. Отразете това на схемата.
• Къде по Земята условията за наблюдение на кометата биха били най-благоприятни?
Решение:
Кометите имат два типа опашки – йонна и прахова. Йонната опашка се състои от йонизирани атоми и молекули и направлението й се определя предимно от налягането на слънчевата светлина. Тя е насочена в посока, противоположна на посоката към Слънцето. Праховата опашка се състои от частици, изхвърлени от ядрото на кометата и направлението й се определя от гравитационното притегляне на частиците от Слънцето и частично от налягането на слънчевата светлина. Частиците отделени от ядрото имат леко различаващи се скорости и започват да се движат по елиптични орбити с различен ексцентрицитет. Затова те образуват широка опашка, която често изглежда извита по направление на новите орбити на частиците. Тези нови орбити, обаче, или лежат в равнината на орбитата на кометата, или са разпределени по наклон, сравнително симетрично спрямо нея. Тъй като орбитата на разглежданата комета лежи в равнината на еклиптиката, то огъването на кометната опашка ще бъде в същата равнина и няма да се забелязва от Земята. И двете опашки ще се проектират на небесната сфера по направление на еклиптиката.
На 30 септември Слънцето току що е подминало есенната равноденствена точка, в която се пресичат небесният екватор и еслиптиката. То вече е слязло под небесния екватор и има отрицателна деклинация. Еклиптиката, пресичаща небесния екватор, е наклонена спрямо него на ъгъл ε = 23°26′. Наклонът на екватора към източния хоризонт е α = 90° – φ , където j е географската ширина на мястото. Пресмятаме и получаваме за наклона на еклиптикта към хоризинта γ = α + ε = 69°36′ . Под такъв ъгъл спрямо хоризинта ще се вижда и опашката на кометата.

Рефракцията повдига точки, намиращи се на 36′ под хоризонта, до нивото на хоризонта. Точки, намиращи се на по-голяма височина, се повдигат на по-малък ъгъл. Вследствие на това характерните линии на небесната сфера се деформират забелижимо в близост до хоризонта. Подобно на еклиптиката ще се деформира и опашката на кометата.

Най-добри условия за наблюдения на една комета има на места, от които височината на кометата над хоризонта е най-голяма. Тъй като кометата отстои от Слънцето по линия, проектираща се върху еклиптиката, най-удобни за наблюдения ще са места, за които еклиптиката е перпендикулярна на хоризонта. В близост до момента на есенно равноденствие, рано сутрин, еклиптиката е почти перпендикулярна на хоризонта за точки от земната повърхност близки до северната тропична окръжност. Освен че главата на кометата ще е най-високо, там опашката на кометата ще бъде насочена право нагоре, в посока перпендикулярна на хоризонта.
3 задача. Окултация. Опишете качествено при какви условия би могла да се наблюдава най-продължителната окултация (покритие) на звезда от Луната. Отчетете всички възможни фактори.
Решение:
Понеже звездите са много далеч от нас, то можем да считаме, че от тях към земния наблюдател идват успоредни лъчи. Това означава, че сянката на Луната, проектирана върху равнина, перпендикулярна на звездните лъчи, има формата и размерите на самата Луна, независимо от разстоянието между Луната и равнината. Ако разгледаме централна окултация, то докато тя трае, лунната сянка се премества на един свой диаметър, който, както вече отбелязахме, е равен на размерите на Луната. Следователно, продължителността на окултацията ще зависи само от отностителната скорост на лунната сянка спрямо наблюдателя. Колкото по-малка е относителната скорост, толкова по-дълго време ще трае окултацията. Затова първите фактори, които ще разгледаме, влияят именно на тази скорост. Когато наблюдателят се намира на различни места по Земята, обаче, лунната сянка ще се проектира върху участъци от земната повърхност, които са под различен наклон спрямо лъчите от звездата. Лунната сянка ще бъде издължена в определено направление. Отначало ще разглезаме случая, когато окултацията става при положение на Луната, което близко до горна кулминация за мястото на наблюдение. Тогава, общо взето, лунната сянка ще бъде издължена по направление, перпендикулярно на относителното движение на Луната, и това издължаване няма да влияе на продължителността на окултацията.
Първият важен фактор е географската ширина на наблюдателя. Както е известно, Луната обикаля около Земята в същата посока в която Земята се върти около оста си. Следователно, точките от земната повърхност „догонват” лунната сянка. Това означава, че най-малка скорост би имала лунната сянка при наблюдение на окултация от екваториалните части на Земята. Там скоростта на околоосно въртене е най-голяма и относителната скорост на лунната сянка ще е най-малка. Това е и причината слънчевите затъмнения да са най-продължителни в тези области.
Вторият важен фактор е разстоянието Земя – Луна. Съгласно втория закон на Кеплер, колкото по-далеч е Луната от нас, толкова по-бавно се движи по орбитата си. Следователно, когато е в апогей и се движи най-бавно, то и сянката й ще има най-малка скорост по земната повърхност. Това означава, че тогава и окултациите ще са по-подължителни.
Друг фактор, който влияе, е начинът по който Луната се движи спрямо небесните паралели (които са успоредни на земните). Когато тя има минимална или максимална деклинация, тя се движи успоредно на тях, съответно и успоредно на въртенето на Земята около оста й. Следователно, тогава относителната й скорост спрямо земния наблюдател би била по-малка и биха се наблюдавали и по-продължителни покрития на звезди.
Възможно е, обаче, окултацията да се случи, когато Луната не е близо до горна кулминация. Всъщност, в такива случаи би имало удължение на сянката на Луната общо взето в посока, благоприятстваща по-голямата продължителност на окултацията. По времето малко след изгрева или малко преди залеза на Луната това удължение на нейната сянка би било значително. Но с подобен фактор тогава би се увеличила и относителната скорост на сянката спрямо земната повърхност. Следователно тези обстоятелства не са от значение при оценката на продължителността на окултацията.
4 задача. Спътник. Изкуствен спътник на Земята се движи по екваториална орбита в същата посока, в която се върти Земята.
• При какви височини над земната повърхност за наблюдател на екватора спътникът ще изгрява от изток и при какви височини ще изгрява от запад?
• Отговорете на същия въпрос в случая, когато спътникът се движи по своята орбита в посока обратна на въртенето на Земята.
Решение:
Спътник с право движение би бил наблюдаван да изгрява от запад и да залязва на изток, ако неговата ъглова скорост е по-голяма от ъгловата скорост на точка от земната повърхност. Това e изпълнено, когато неговият орбитален период е по-малък от периода на околоосно въртене на Земята. Орбиталният период на спътника в зависимост от височината може да се получи чрез третия закон на Кеплер:

където R е радиусът на Земята, h – височината на спътника над екватора, T – неговият период, M – масата на Земята, a γ гравитационната константа.
Когато спътникът се намира на височина, при която неговият орбитален период е равен на периода на околоосно въртене на Земята, ъгловите скорости на двете тела са еднакви и той винаги стои в една и съща точка от небесната сфера. Такъв спътник се нарича геостационарен и неговата височина е 35 786 km.
При още по-големи височини спътникът има орбитален период по-голям от едно звездно денонощие (времето, за което Земята прави една пълна обиколка около оста си) и ние го наблюдаваме да изгрява от изток и да залязва на запад.
Когато спътникът се движи обратно на въртенето на Земята, т.е. от изток на запад, той винаги изгрява от изток и залязва на запад, защото относителната ъглова скорост на двете тела е сума от ъгловите скорости на спътника и Земята, следователно винаги по-голяма от тази на Земята.
5 задача. Голямата мечка. След наблюдателните занятия в Борисовата градина вие изоставате от групата и се загубвате. В тъмнината към вас се приближава фосфоресциращ участник в Междузвездната олимпиада по астрономия. Бързо се сприятелявате и разбирате, че той идва от Голямата мечка. Предлага ви загадка. Разгледайте внимателно схемите с видимите и абсолютните звездни величини на звездите от съзвездието. Родното слънце на госта е най-далечната от тези звезди. Тоя е тя? Обяснете вашия отговор.
Решение:
Разликата между видимата и абсолютната звездна величина (m – M) се нарича модул на разстоянието и представлява еднозначна функция на истинското разстояние r до даден космически обект в парсеци:
m – M = 5log(r) – 5
Лесно може да се види, че колкото е по-голям модулът на разстоянието на дадена звезда, толкова по-далечна е тя. Когато той е отрицателен, звездата е на по-малко от 10 pc, а когато е положителен, на разстояние по-голямо от 10 pc.
Следователно, за да открием родната звезда на участника в Междузвездната олимпиада, трябва да потърсим звездата, чиято разлика между видима и абсолютна звездна величина е най-голяма. От схемата се вижда, че това е Алкаид.
Справочни данни:
Гравитационна константа γ = 6.67 × 10-11 м3/кг.с2
Екваториален радиус на Земята 6378 км
Маса на Земята 6 × 1024 кг
Ученици стардша възраст (до 18 г.)
1 задача. Геостационарен спътник. През 2030 г. участници в школата за подготовка за Международната олимпиада по астрономия в Хасково (φ = 41°55′, λ = 25°33′) монтират сателитна антена, с която ще приемат лекциите на професор Йовелина Зинкова, предавани чрез геостационарен спътник. Спътникът е в посока юг. На каква височина над хоризонта трябва да е насочена антената?
Решение:
Геостационарен се нарична спътник, който стои неподвижен спрямо земната повърхност. Това е възможно само в случай, когато орбиталният му период е точно равен на периода на околоосно въртене на Земята (Tзв = 23h56m04s), а орбитата му е разположена точно над земния екватор.
Нека първо да изчислим радиуса на орбитата на такъв спътник. Съгласно третия закон на Кеплер, ако M3 = 6×1024 kg е земната маса, то:
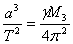
където γ = 6.67 × 10-11 м3/кг.с2 е гравитационната константа.
Оттук намираме:

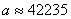 km km
Височината на спътника над земната повърхност е  35 857 km, където R е земният радиус. 35 857 km, където R е земният радиус.

На чертежа с точка В е означено положението на геостационарния спътник, а с точка А положението на град Хасково. Ъгълът АОВ е всъщност географската ширина на наблюдателния пункт j. Допирателната AD към земната повърхност в точка А е хоризонтът за наблюдател, разположен там. Ъгълът DAB е търсената височина на спътника над хоризонта h. Понеже спътникът се намира на крайно разстояние от Земята, което по порядък е сравнимо с нейния радиус, то наблюдател, който не е разположен на земния екватор, няма да вижда спътника на небесния екватор. В случая, участниците в школата, които се намират в северното полукълбо, ще го виждат южно от небесния екватор. Ако означим деклинацията на спътника с δ, то за търсената височина можем да запишем:
h = 90° – φ – δ
Тази деклинация е равна на ъгъла ОВА на чертежа. Отсечката ОВ е равна на радиуса на орбитата на спътника. От точка А спускаме перпендикуляр към нея (АС). Пресмятаме разстоянията АС и ОС:
АC = R.sin φ= 4261 km
ОC = R.cos φ = 4746 km.
Следователно:
BC = OB – OC = R + H – OC = 37 489 km.
Тъй като tg OBA = AC / BC, можем да намерим ъгъла OBA:
<ОВА = δ = 6°.4844
Това означава, че от Хасково геостационарният спътник ще се вижда на около 6°30′ под небесния екватор. Оттук намираме:
h = 90° – φ – δ ≈ 41°36′.
2 задача. Двойна звезда. (20т.) Двойната система 42 Com се състои от две еднакви звезди от Главната последователност на диаграмата на Херцшпрунг-Ръсел, всяка със звездна величина 5.22m и спектрален клас F5. Паралаксът на 42 Com е 0.057″. Наклонът на орбиталната плоскост на двете звезди към зрителния лъч е близък до 0°, макар и не достатъчно, за да се наблюдава системата като затъмнително-двойна звезда. Относителната орбита на едната звезда около другата е елипса с ексцентрицитет 0.37. Голямата й полуос е насочена към Земята.
• Земният астроном Делян Лафчиев си разменя данни за тази система със своите любезни виолетови колеги от планетата Х, намираща се на същото разстояние от 42 Com, както Земята, но в перпендиклярна посока. От тях той знае, че голямата полуос на относителната орбитата е с видим ъглов размер 0.66″ и че те я наблюдават като затъмнително двойна звезда с централни затъмнения. Нарисувайте схематично как би изглеждала кривата на изменение на блясъка, получена от тази далечна планета.
• Намерете минималния ъгъл, под който орбиталната плоскост може да бъде наклонена към зрителния лъч за земния наблюдател, така че да не се наблюдават затъмнения в двойната система.
• Колко би продължавало затъмнението на едната звезда от другата за нас при положение, че наклонът на орбиталната плоскост към зрителниа лъч е 0°? Орбиталният период на системата е 26 години.
Решение:
Относителната орбита се получава, когато разглеждаме движението на звездите в система, в която едната звезда е неподвижна, а другата обикаля около нея. Щом голямата ос на относителната орбита на двойната система е насочена към нас, то тя ще бъде перпендикулярна на лъча на зрение за наблюдателя от планетата X.

Тъй като орбитата е силно елиптична, то за извънземния наблюдател, намиращ се в посока перпендикулярна на голямата ос на двойната звезда, в кривата на блясъка вторичният минимум няма да бъде симетричен спрямо главните минимуми. Както се вижда от схемата, от момента, когато звездата В закрива звездата А, до момента, когато звездата В премине зад звездата А, минава значително по-малко време, отколкото от момента, когато звездата В преминава зад звездата А, до момента, когато звездата В отново закрива звездата А. Причината е не само в различния път по орбитата, който звездата В преминава в двата случая, но и в това, че съгласно втория закон на Кеплер, в периастъра орбиталната скорост е по-голяма, отколкото в апоастъра на орбитата. Вторичният и главният минимум са остри и еднакви по амплитуда, защото двете компоненти са еднакви. Строго погледнато обаче, графиките на самите минимуми няма да са симетрични. Спадането на блясъка при главния минимум ще е малко по-бавно, отколкото покачването на блясъка, понеже орбиталната скорост на звездата В по време на този минимум ще нараства с приближаването към периастрия. При вторичния минимум скоростта ще намалява с отдалечаването от периастрия и неговата графика ще бъде огледална на главния минимум.
За извънземния наблюдател кривата на блясъка ще изглежда по следния начин:
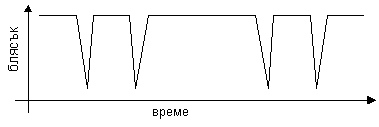
Щом звездите са от спектрален клас F5 и се намират на главната последователност, то те са от V клас светимост. От таблицата с астрофизичните характеристики на звездите виждаме, че такива звезди имат среден радиус 1.3 слънчеви радиуса или 900 000 км. Най-малкият възможен ъгъл, при който не се наблюдават затъмнения, се определя от следния чертеж:
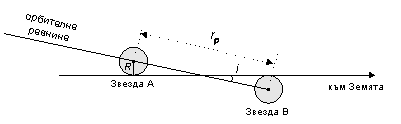



където а е голямата полуос на орбитата в астрономически единици, е е ексцентрицитетът,  ъгловият размер на голямата полус, видима от разстоянието, на което се намираме, ъгловият размер на голямата полус, видима от разстоянието, на което се намираме,  е паралаксът на двойната система. Заместваме и получаваме за максималния наклон на орбитата следния израз: е паралаксът на двойната система. Заместваме и получаваме за максималния наклон на орбитата следния израз:
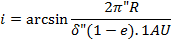
i =5′40″
Минималният възможен ъгъл на наклона на орбитата на двойната звезда спрямо зрителния лъч, при който няма да наблюдаваме затъмнения, е приблизително 6 дъгови минути.
Времето на едно централно затъмнение ще бъде равно на времето, за което едната звезда изминава два пъти своя диаметър. Главният и вторичният минимум ще бъдат различни по продължителност в зависимост от това дали затъмнението се случва в периастъра на относителната орбита, или в апоастъра.


T1 = 51 h
T2 =111 h
Кривата на блясъка би изглеждала по следния начин:

3 задача. Вега в зенита. При посещение в Националната астрономическа обсерватория – Рожен посетител с бегли астрономически познания задава въпрос: „Звездата Вега винаги ли се наблюдава в зенита?” Нека си представим, че тази абсурдна ситуация е реална и че Вега (α = 18h37m , δ = +38°47′) наистина винаги се наблюдава в зенита за НАО – Рожен.
• Как трябва да се промени околоосното движение на Земята, за да стане това?
• Как ще се редуват тогава денят и нощта? Кога за НАО – Рожен ще започва денят и кога – нощта?
• С какви дрехи трябва да се обличат астрономите в обсерваторията през юни-юли? А как трябва да се обличат хората в щата Аризона по същото време?
• Коя звезда ще бъде в зенита за НАО – Рожен след 2000 години?
Решение:
За да бъде някоя звезда постоянно в зенита за което и да е място по Земята, то би трябвало с течение на времето видът на небето да не се променя. Това (при сегашното околоосно въртене на Земята) е възможно само ако звездата се намира в някой от небесните полюси, а наблюдателят на някой от земните полюси. Вега не е в никой полюс и затова единствената възможност да остава винаги в зенита е звездите да стоят неподвижни спрямо Рожен. Това означава, че Земята винаги има една и съща ориентация спрямо тях, т.е. не се върти около оста си. При това положение звездното денонощие има безкрайна продължителност и за никое място по Земята звездното небе няма да се променя.
Въпреки че звездите няма да се движат по небето Слънцето ще извършва годишното си движение на фона им, защото то се дължи на обикалянето на Земята по орбитата й. Неговият видим път (еклиптиката) е голям кръг от небесната сфера. Следователно, тя ще се пресича с хоризонта в две диаметрално противоположни точки. Когато Слънцето се намира в тези точки, то ще изгрява и ще залязва за НАО Рожен. От тук следва, че при това положение денят и нощтта ще имат еднаква продължителност по шест месеца.
Понеже Вега е в зенита и има ректасцензия 18h36m56s, то Слънцето ще е в горна кулминация в момента, когато и неговата рекасцензия е такава. Както знаем, тя по време на зимно слънцестоене е точно 18h, и се изменя с около 4 минути на ден. Това означава, че Слънцето ще е в горна кулминация около 9 дни след зимното слънцестоене или около 1-ви януари. Съответно изгревът му ще е 3 месеца преди това или около 1-ви октомври, а залезът около 1-ви април.
Понеже Слънцето ще залязва на 1-ви април, то цяло лято няма да е над хоризонта. Съответно няма да огрява обсерваторията на Рожен и тогава там би трябвало да е много студено. Астрономите ще трябвада се обличат топло и непрекъснато ще е нощ – няма да има почивка за тях от наблюденията (освен ако не се заоблачи небето). През зимата то ще е постоянно над хоризонта и затова тогава би трябвало да е топлият сезон за това място, въпреки че ще Слънцето ще е ниско над хоризонта.
Аризона се намира приблизително на противоположна географска дължина спрямо Рожен. Това означава, че през летните (от сегашна гледна точка) месеци, докато на Рожен е нощ, то в Аризона ще е ден. Освен това, Слънцето ще е високо над хоризонта, защото ще е в северната небесна полусфера. Следователно там лятото ще е много горещо, а зимата много студено.
Както се убедихме, видът на небето никога няма да се променя. Единственото, което ще се случва, са изгревът и залезът на Слънцето през интервал от време 6 месеца.
Все пак съзвездията, които са на небето, биха могли да се променят поради влиянието на прецесията. Прецесия обаче няма да има, защото няма да има въртене на Земята около оста, т.е. няма да има ос, която да прецесира.
Би могло Вега да е винаги в зенита и при условие, че оста на Земята е насочена към нея. В такъв случай Рожен ще се намира точно на северния географски полюс на Земята. Знаем, че деклинацията на северния небесен полюс е +66,5°, а деклинацията на Вега е 38°. Следователно, наклонът на земната ос спрямо равнината на Екватора в този случай ще бъде около 29°. Наблюдател на Рожен ще вижда как звездите се движат успоредно на хоризонта му, който ще съвпада с небесния екватор в този случай.
Понеже Рожен се намира в полюса на Земята, то за наблюдател там Слънцето ще е над хоризонта в продължение на половин година. Пресечните точки на еклиптиката с хоризонта ще се същите като в предния случай, следователно и датите на изгрев и залез ще са същите. Съответно и температурите ще са същите като в предния случай. Променя се, обаче ситуацията с Аризона. Тя е приблизително на около 90° от България, измервано по геодезичната линия между двете. Следователно при това положение, тя ще е на земния екватор. Затова там през месеците януари и юли (през които Слънцето е близо до своето слънцестоене) то ще се изкачва максимално ниско над хоризонта по пладне, защото е максимално далеч от небесния екватор.
Тук вече Земята се върти около оста си, т.е. прецесия ще има. Наклонът на оста й е малко по-голям отколкото е сега. Да приемем, че периодът й на прецесия е приблизително същият като сега – 26 000 г. Посоката също би могло да се очаква да бъде същата, т.е. северният небесен полюас ще се движи в посока обратна на годишното движение на Слънцето по еклиптиката. След 2000 години то ще се е преместило на около 1/12 част от прецесионния си път и ще се намира в северната (от сегашна гледна точка) част на съзвездието Херкулес.
4 задача. Небе в звезден куп. Общата звездна величина, характеризираща светенето на цялото видимо нощно небе заедно със звездите на Земята, е –7m . След като е изучил всички съзвездия на земното небе, астрономът Констанин Гундев отлита към странна планета в странен кълбовиден куп от обратната страна на Галактиката, тъй като само на такова място вече разучаването на звездите е достойна задача за него. Радиусът на звездния куп е 20 рс. Всички звезди в него имат абсолютна звездна величина 3m . Купът съдържа 200 000 звезди, равномерно разпределени в целия му обем. Каква ще бъде общата звездна величина, характеризираща светенето на нощното небе на странната планета?
Решение:
Нека Е10’ е осветеността, която една звезда с абсолютна звездна величина 3m създава на разстояние 10 рс. Да пресметнем общата осветеност Еr , която създават за наблюдател в центъра на звездния куп всички звезди, намиращи се в сферичен слой от купа с радиус r и малка дебелина Δr.
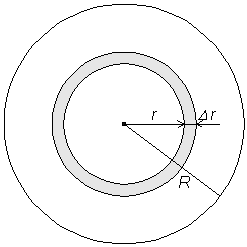
Тъй като дебелината е малка, приблизителният обем на този слой пресмятаме като произведение на площта на вътрешната страна на слоя и дебелината:

Да означим с  общия брой звезди в звездния куп, а с R – неговия радиус. Обемът на целия куп ще бъде: общия брой звезди в звездния куп, а с R – неговия радиус. Обемът на целия куп ще бъде:

Броят звезди, съдържащи се в тънкия слой ще бъде:

Осветеността, която създава една звезда от слоя за наблюдател в центъра на звездния куп, ще бъде:

където r е в парсеци. Общата осветеност от всички звезди в слоя ще бъде:


Тук R и Δr също трябва да са в парсеци. Интересното в този резултат е, че както се оказва, общата осветеност от всички звезди в сферичния слой не зависи от неговия радиус r . Това означава, че ако разделим кълбовидния куп на множество такива концентрични слоеве със същата дебелина, но с различни радиуси, то звездите от всеки такъв слой ще имат еднакъв принос към общата осветеност, създавана в центъра на купа. Тъй като осветеността от даден слой е право пропорционална на дебелината му Δr, то общата осветеност от всички звезди в купа ще намерим, като сумираме приносите на всички слоеве:


Звездната величина m , която съответства на тази осветеност, пресмятаме по формулата на Погсън. Сравняваме я с абсолютната звездна величина на една звезда от купа (3m):
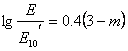


Има още един фактор, който създава фонова осветеност. Това са звездите от Галактиката, разположени извън купа. В условието се казва, че купът е от другата страна на Млечния път. Следователно можем да приемем, че там има същата концентрация на звезди, каквато и в околностите на Слънцето, т.е. че те дават същата сумарна звездна величина, равна на –7m. Това съответства на осветеност около 16 пъти по-малка отколкото от звездите в купа. Можем да смятаме, че приносът на звездите извън купа към общия блясък на небето няма да е съществен. Поради това заключаваме, че общата яркост на фона ще е около -10m.
За да се получи по-точна оценка за реален звезден куп, трябвада се отчете, че звездите не са от една и съща абсолютна звездна величина и не са равномерно разпределени в целия обем на купа.
5 задача. Ретроградно движение. Както е известно, планетите извършват видимо движение на фона на звездите, при което понякога описват „примки” – за определено време обръщат посоката си на движение и вместо от запад на изток, както обикновено, те се движат от изток на запад. За всяка планета продължителността на това ретроградно движение е различна.
• Обяснете качествено как ще се изменя интервалът от време, през който един обект има ретроградно движение, с увеличаване на разстоянието му от Слънцето.
• Каква е максималната стойност на този интервал от време?
Решение:
Сложните видими пътища, които планетите описват на фона на звездите, се обясняват с това, че те се движат около Слънцето, а ние ги наблюдаваме от движещата се около Слънцето Земя. В определени интервали от време планетите имат ретроградното движение. За външните планети ретроградното движение се наблюдава около опозицията, а за вътрешните около долното съединение.
Вътрешните планети се движат около Слънцето с по-големи ъглови и линейни скорости, отколкото Земята. На Фиг.1 са показани последователните взаимни положения на Земята и една вътрешна планета през равни интервали от време. Условно е изобразено и видимото преместване на планетата по небето за земния наблюдател. Отначало имаме видимо движение в права посока. Когато Земята достигне до точка 1 от орбитата си, посоката на видимо движение на планетата се обръща. Проекцията на планетата на фона на звездите в този момент, условно изобразена с точка 1’, се нарича точка на стоене. Това е, защото около тази точка планетата се премества много бавно и сякаш „стои” на едно място на звездното небе. Тогава започва ретроградното движение на планетата и приключва в точка 2’, също точка на стоене, след което посоката отново се обръща и планетата възобновява правото си движение. 
Фиг. 1
От значение за това явление е съотношението на големините и посоките на орбиталните скорости на планетата и Земята в различни моменти. Точките на стоене съответстват на моментите, когато планетата има относителна скорост спрямо Земята, насочена изцяло по правата Земя-планета (зрителния лъч), т.е. когато напречната на зрителния лъч компонента на тази относителна скорост е нула. Нека с VT означим скоростта на Земята по нейната орбита, а с VP – скоростта на планетата в даден момент. Относителната скорост на планетата спрямо Земята ще бъзе:

На Фиг. 2 е представено взаимно положение на Земята и планетата, отговарящо на точка на стоене.

Фиг. 2
Ретроградното движение става в интервала от време, когато планетата, движейки се почти успоредно със Земята, я „изпреварва”, понеже има по-голяма скорост. Колкото по-далеч е планетата от Слънцето, толкова по-близка е нейната скорост до земната орбитална скорост и положенията, при които тя „изпреварва” Земята, ще са съсредоточени в по-малък сектор от орбитата. Следователно интервалите от време с ретроградно движение ще се съкращават, клонейки към нула с приближаване към земната орбита. Колкото планетата е по-близо до Слънцето, толкова по-продължителни ще са интервалите от време с ретроградно движение.
Външните планети се движат около Слънцето с по-малки ъглови и линейни скорости, отколкото Земята. На Фиг. 3 може да се види как се получава ретроградно движение при наблюдение на външна планета. Точките на стоене също са отбелязани с 1’ и 2’. 
Фиг. 3
На Фиг. 4 е показана относителната скорост на външна планета спрямо Земята, когато планетата е в точка на стоене.

Фиг. 4
Ретроградното движение в този случай става в интервала от време, когато планетата, движейки се почти успоредно със Земята, „изостава” от нея, понеже има по-малка скорост. Колкото по-близо е планетата до Слънцето, толкова по-близо е тя и до Земята, и нейната скорост е по-близка до земната орбитална скорост. Затова интервалите от време, когато тя ще „изостава” от Земята, ще са по-кратки, като ще клонят към нула с приближаване към орбитата на Земята. Колкото по-далеч е планетата от Слънцето, толкова по-дълги ще са тези интервали.
Да разгледаме планета, която е много по-далеч от Слънцето, отколкото Земята. Тогава нейната орбитална скорост ще е толкова малка, че в рамките на година или повече можем да считаме планетата почти неподвижна в една точка от нейната орбита. Тогава видимото движение на планетата на фона на звездите ще се определя главно от движението на Земята около Слънцето. Видимият път на планетата ще изглежда като малки примки, близко разположени една до друга и с ъглов размер, приблизително равен на видимия от планетата диаметър на земната орбита (Фиг. 5). Интервалите от време с ретроградно движение ще бъдат приблизително равни на половин земна година и това е максималната им възможна продължителност.

Фиг. 5
Справочни данни:
Гравитационна константа γ = 6.67 × 10-11 м3/кг.с2
Екваториален радиус на Земята 6378 км
Маса на Земята 6 × 1024 кг
Константа на Стефан-Болцман s = 5.67 × 10-8 Вт/м2К4 |
|