|
МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО
И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА
ПО АСТРОНОМИЯ
Х НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
http://astro-olymp.org
ІV кръг - решения
Ученици младша възраст (до 15 г.)
1 задача. Метеорният поток Дракониди действа през месец октомври, а η-Аквариди – през месец май.
От кой поток на Земята се наблюдават по-бързи метеори? Обяснете своя отговор.
За по-бързия от двата потока скоростта на метеорите относно Земята е 66 km/s, а за по-бавния – 23 km/s. Пресметнете с какви скорости се движат метеорните частици от всеки от двата потока относно Слънцето.
Решение: В края на април и през май Слънцето се намира в зодиакалния знак Телец (Бик). Поради прецесията на земната ос обаче, понастоящем в този период на годината то е в съзвездието Овен. Радиантът на потока η-Аквариди се намира във Водолей. Това е посоката, от която метеорните частици от роя на η-Акваридите идват към Земята. Тъй като Водолей се намира на две зодиакални съзвездия по еклиптиката преди Овен, то това означава, че метеорните частици от η-Акваридите се движат почти насрещно на орбитaлното движение на Земята. Затова относителната скорост на метеорите от този поток спрямо земния наблюдател трябва да е голяма.
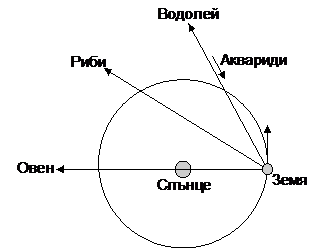
В съзвездието Дракон се намира Северният еклиптичен полюс. Следователно частиците от роя на Драконидите идват към Земята от направление близко до перпендикулярното на нейното орбитално движение. Затова Драконидите трябва да са по-бавни за земния наблюдател, отколкото η-Акваридите.
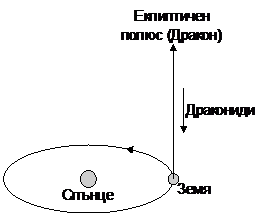
Скоростта на движение на Земята около Слънцето определяме от радиуса на земната орбита r и орбиталния период на Земята Т= 1 година:
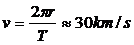
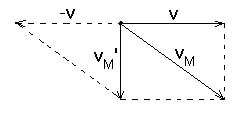
Тъй като Драконидите са по-бавният поток, то тяхната скорост относно Земята е 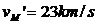 . Скоростта им относно Земята vM’ е перпендикулярна на земната скорост v. Скоростта им относно Слънцето намираме с помощта на Питагоровата теорема: . Скоростта им относно Земята vM’ е перпендикулярна на земната скорост v. Скоростта им относно Слънцето намираме с помощта на Питагоровата теорема:
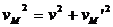
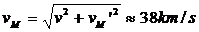
Но Дракон е голямо съзвездие и ние не знаем къде точно в него е радиантът на Драконидите. Следователно не разполагаме с достатъчно данни, за да опредлим точно скоростта на метеорните частици относно Слънцето.
За η-Акваридите можем съвсем приблизително да оценим, че скоростта им относно Слънцето е:
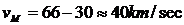
(Получените скорости са приблизителни, тъй като не са дадени точните координати на радиантите и следователно не може да се намери точното направление на движение на метеорните частици. Освен това дадените скорости на метеорните частици относно Земята са определени от наблюденията на метеорите. Техните стойности са повлияни от гравитационното привличане, което Земята оказва върху приближаващите се към нея частици. Това, обаче, не е отчетено в решението на задачата. При големи скорости на метеорните частици, от порядъка на десетки километри в секунда, промените в хелиоцентричните скорости, поради неотчитане на гравитационното въздействие на Земята, са много малки – от порядъка на 1-2 km/s.)
2 задача. Младият астроном Даниел Цветков стои в къщи с навехнат крак и наблюдава с телескоп през прозореца Юпитер в противостоене. В 0h UT Даниел наблюдава затъмнение на спътника Калисто от сянката на Юпитер. После той се заема да пресмята кога ще се случат следващите затъмнения.
Пресметнете периода между две затъмнения на Калисто, като знаете, че орбиталният период на спътника около планетата е 16,689 денонощия.
По-късно, когато Юпитер вече е в източна квадратура, Даниел отново наблюдава затъмнения на Калисто, но установява, че те настъпват с 455 s закъснение спрямо изчислените по предишните данни. Той не знае, че с подобни наблюдения в 19 век датският астроном Оле Рьомер е определил скоростта на светлината.
Определете тази скорост и вие.
Решение: Ориентацията на сянката на Юпитер зависи от положението на планетата по нейната орбита. Ето защо, ако ТK е орбиталният период на Калисто около Юпитер, а ТЮ е орбиталният период на Юпитер около Слънцето, то периодът между две последователни затъмнения на Калисто ТЕ намираме от съотношението:
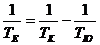
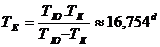

Когато Юпитер е в противостоене, разстоянието му до Земята е r= r1– r2 ≈ 628,7×106 km.
където r1 e радиусът на орбитата на Юпитер, а r2 e радиусът на земната орбита. Нека х е разстоянието от Земята до Юпитер в квадратура. От чертежа се вижда, че съгласно теоремата на Питагор:
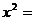 r12 – r22 r12 – r22
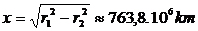
Когато Юпитер е в квадратура, светлината оттам до Земята изминава по-дълъг път, отколкото когато е в опозиция. Удължаването на пътя е: x – r =135,1×106 km.
Именно на това се дължи закъснението с време t= 455 s на моментите на затъмненията на Калисто. Оттук определяме скоростта на светлината:
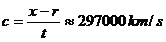
Справочни данни:
Орбитален период на Юпитер – 11,857 години
Радиус на орбитата на Юпитер – 778,3×106 km
Радиус на земната орбита – 149,6×106 km
3 задача. Да предположим, че в деня на пролетното равноденствие планетата Венера се оказва в точката на максимална източна елонгация (на 47° от Слънцето).
На какви географски ширини по Земята Венера ще може да се вижда в небето след като залезе Слънцето?
Ще може ли някъде (и ако да – къде) Венера да се наблюдава като незалязващо светило? Обяснете своя отговор.
Считайте, че орбитата на Венера лежи в равнината на еклиптиката.
Решение: Венера е в максимална източна елонгация, т.е. тя е източно от Слънцето. Самото Слънце се движи по еклиптиката от запад на изток. Следователно Венера се намира в област от еклиптиката, в която Слънцето ще бъде след няколко месеца. Понеже Слънцето е близо до пролетната равноденствена точка, то Венера се намира в северната небесна полусфера. Тя отстои от Слънцето на 47° и следователно се намира около средата между точките на пролетно равноденствие и на лятното слънцестоене.

С отдалечаване от пролетната равноденствена точка, деклинацията на една планета, намираща се върху еклиптиката, не би нараствала равномерно. Отначало тя ще расте по-бързо, а после – съществено по-бавно. Оттук следва, че деклинацията на Венера трябва да е над половината от наклона e = 23°26′ на еклптиката към небесния екватор, т.е. с няколко градуса над +12°. Следователно Венера ще бъде видима от цялото северно полукълбо и от голяма част от южното. Всъщност за северното полукълбо видимостта й ще бъде по-добра, отколкото за южното. Както се вижда от фигурата, отнасяща се до наблюдател в северното полукълбо на Земята, там еклиптиката ще сключва по-голям ъгъл с хоризонта, т.е. Венера ще е по-високо на залез Слънце. Поради положителната си деклинация, т.е. поради това, че Венера се намира в северната небесна полусфера, за наблюдател в южното полукълбо на Земята тя ще бъде по-ниско над хоризонта, а в малка област около южния полюс на Земята тя ще бъде неизгряващо небесно светило и винаги ще бъде под хоризонта.
Като незалязващо светило Венера ще се вижда в малка област около Северния полюс с радиус, съществено по-малък от 12°.
4 задача. В таблицата са дадени данни за изменението на видимата звездна величина m на обект от Слънчевата система в продължение на пет години. Постройте графика, показваща това изменение.
Кога приблизително се очаква да бъде следващият период на максимален блясък на обекта?
Кой е този обект?
Защо в периодите, когато обектът е най-ярък, звездната му величина не достига една и съща стойност?
Какво може да се очаква от предстоящия нов период на максимален блясък на обекта – дали тогава той ще достигне до по-голяма или до по-малка яркост в сравнение с предишните два максимума? Обяснете своя отговор.
Години |
Месеци |
m |
2002 |
1 |
0,8 |
|
4 |
1,5 |
|
7 |
1,8 |
|
10 |
1,8 |
2003 |
1 |
1,5 |
|
4 |
0,5 |
|
6 |
-0,7 |
|
7 |
-1,5 |
|
8 |
-2,4 |
|
9 |
-2,9 |
|
10 |
-2,1 |
|
11 |
-1,2 |
|
12 |
-0,4 |
2004 |
1 |
0,2 |
|
4 |
1,4 |
|
7 |
1,8 |
|
10 |
1,7 |
2005 |
1 |
1,6 |
|
4 |
0,9 |
|
7 |
-0,1 |
|
8 |
-0,5 |
|
9 |
-1 |
|
10 |
-1,7 |
|
11 |
-2,3 |
|
12 |
-1,6 |
2006 |
1 |
-0,6 |
|
4 |
1,2 |
|
7 |
1,8 |
|
10 |
1,8 |
Решение: Построяваме графика на изменението на блясъка на обекта от времето. Определяме моментите на максимален блясък на обекта:
9. 2003 г.; 11. 2005 г.
Периодът между два съседни максимума е около 2 години и 2 месеца. Оттук можем да направим извода, че обектът е планетата Марс и че максимумите на видимия й блясък (минимумите на видимата звездна величина) съответстват на моментите, когато Марс е най-близо до Земята – в противостоене. Марсианската орбита е значително сплесната. Поради това разстоянието от Марс в противостоене до Земята варира в доста широки граници. Ето защо при всяко противостоене планетата има различен максимален видим блясък. Виждаме, че през 2003 г. максимумът е по-висок отколкото този през 2005 г. Тогава Марс, както си спомняме, беше близо до перихелия си (велико противостоене) и затова разстоянието от Земята до него беше близко до минималното. Предполагаме, че следващият максимум на блясъка ще настъпи също около 2 години и 2 месеца след втория максимум на графиката, т.е. през януари 2008 г. (В действителност, както може да се провери в Астрономическия алманах, следващото противостоене на Марс е в края на декември 2007 г.). Тъй като периодът от едно противостоене до следващото е около 2 години и 2 месеца, то при следващото противостоене Земята е отместена по орбитата си с около 60° спрямо предходното. Това означава, че по време на противостоенето си през 2005 г. Марс е бил на около 60° от перихелия на своята орбита, а по време на следващото противостоене ще е още по-далеч от него. Затова тогава блясъкът му ще е още по-слаб и следващият максимум на блясъка на планетата би трябвало да бъде още по-нисък от предните два, показани на графиката.
|
|