МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО
И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА
ПО АСТРОНОМИЯ
VІІІ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
http://astro-olymp.org
IІІ кръг - решения
Ученици от 11-12 клас
1 задача.
Малката планета № 887 (астероидът Алинда) обикаля около Слънцето по издължена елиптична орбита. За наблюдател, намиращ се близо до Слънцето, звездната й величина се изменя с амплитуда ΔmА = 5.24m . С каква амплитуда ΔmS ще се променя звездната величина на Слънцето за наблюдател, намиращ се на астероида Алинда?
Решение:
За наблюдател на повърхността на астероида видимата звездна величина на Слънцето ще се променя поради това, че при движевието си по своята издължена елиптична орбита астероидът ще се намира на различни разстояния от Слънцето в различни моменти от време. За наблюдател в близост до Слънцето видимата звездна величина на астероида ще се променя по две причини:
• Поради различното разстояние на астероида до наблюдателя в различни моменти от време;
• Поради различната осветеност на астероида от Слънцето, когато той е различно отдалечен от него.
Нека с r1 и r2 отбележим съответно най-малкото и най-голямото разстояние, на което астероидът може да е от Слънцето, а с Е1 и Е2 – осветеностите, които Слънцето създава на повърхността на астероида при тези две разстояния. Съгласно формулата на Погсон:
 (1) (1)
Освен това е изпълнено съотношението:
 (2) (2)
откъдето получаваме:
 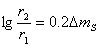 (3) (3)
Осветеността, която астероидът създава от разстояние r1 за наблюдател в близост до Слънцето, е пропорционална на осветеността на астероида от Слънцето и площта S на видимия диск на астероида, и обратно пропорционална на квадрата на разстоянието:

Аналогчно за осветеността, създавана от астероида на разстояние r2 можем да напишем:
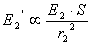
Разделяме почленно двете последни уравнения и като използваме (2), получаваме:

От друга старана:
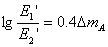
откъдето следва:
 (4) (4)
Като сравним (4) и (3), окончателно пресмятаме:
 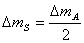

2 задача.
На фигурата е дадена орбитата на звезда около невидимия обект, който се намира в центъра на нашата Галактика. Орбитата е получена в резултат от десетгодишни наблюдения в инфрачервени лъчи с 8.2-метровия телескоп Йепун – един от четирите големи телескопи на Европейската южна обсерватория в Чили. Изключително високата разделителна способност е постигната с помощта на специална система за адаптивна оптика и комбиниране с много точни радионаблюдения.
Положението на централния обект Sgr A* е отбелязано с кръстче, заградено в кръг. Въз основа на данните от фигурата приведете аргументи в полза на твърдението, че този централен обект представлява черна дупка. Приемете, че наклонът на голямата ос на действителната орбита на звездата към плоскостта на чертежа е около 40?.
Справочни данни :
Маса на Слънцето 2 × 1030 kg
Гравитационна константа 6.67 × 10-11 m3 / kg . s2
Решение:
На фигурата е представена проекцията на действителната орбита на звездата върху равнина, перпендикулярна на зрителния лъч за земния наблюдател. Но от разположението на централния обект се вижда, че голямата ос на проектираната орбита е близка до проекцията на голямата ос на истинската елипса. Дължината на голямата полуос на проекцията а ' може да е по-малка или равна на голямата полуос на действителната елипса a . По ІІІ закон на Кеплер:
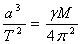
където Т е орбиталният период на звездата, а М е масата на централния обект. Оттук може да се определи масата на този обект:
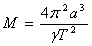
Като имаме предвид, че  , можем да напишем: , можем да напишем:
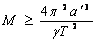
Приемаме, че 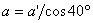 , и получаваме уточнена формула: , и получаваме уточнена формула:
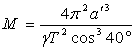
Орбиталният период определяме от фигурата. Както вече споменахме, голямата полуос на видимата орбита е съвсем малко отместена спрямо проекцията на голямата полуос на истинската орбита. Можем да смятаме, че от положението на звездата, наблюдавано около средата между моментите 1994.32 и 1995.53, и положението в момента 2002.33 е изминала приблизително половината от периода. Следователно 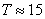 години. Величината a' в километри определяме, като измерим голямата полуос на проектираната орбита в милиметри и използваме дадения на рисунката мащаб: години. Величината a' в километри определяме, като измерим голямата полуос на проектираната орбита в милиметри и използваме дадения на рисунката мащаб: 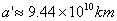 . Получаваме: . Получаваме:
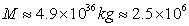 слънчеви маси слънчеви маси
Също използвайки мащаба на чертежа, оценяваме минималното расстояние, на което звездата преминава от централния обект:
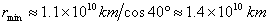 , ,
или около 90 AU . Това е примерно колкото диаметъра на Слънчевата система.
Оценките ни показват, че в центъра на нашата Галактика се намира обект с маса, около 2.5 милиона пъти по-голяма от масата на Слънцето. Тя е съсредоточена в област от пространството с размери не по-големи от размерите на Слънчевата система. При всичко това, както се вижда от снимката вляво от чертежа, практически липсва излъчване на обекта в инфрачервена светлина, или ако има такова, то е по-слабо от излъчването на звездата, чиято орбита изследваме. Можем да предположим, че същото се отнася и до излъчването на обекта във видима светлина. Но както е известно, той е източник на радиоизлъчване, обозначаван като Sgr A . Всички тези аргументи подкрепят твърдението, че обектът представлява черна дупка. Радиусът на Шварцшилд за черна дупка с получената тук маса е
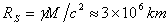 . .
3 задача.
Планета от Слънчевата система се наблюдава в противостоене. Ректасцензията й е α1 = 11 h 03 m . В следващото след противостоенето съединение ректасцензията на планетата е α2 = 11 h 59 m . Коя е тази планета? Защо се получава разлика между орбиталния период на планетата, изчислен по данните от задачата, и действителния й период?
Справочни данни :
Орбитални периоди на планетите от Слънчевата система:
Планета |
Меркурий |
Венера |
Земя |
Марс |
Юпитер |
Сатурн |
Уран |
Нептун |
Плутон |
Период (години) |
0.24 |
0.62 |
1 |
1.88 |
11.9 |
29.4 |
83.7 |
164 |
248 |
Решение:
Щом като планетата може да се наблюдава в противостоене, очевидно тя е външна планета. В противостоене планетата е на 180? от Слънцето. Ако тогава нейната ректасцензия е била α1 = 11 h 03 m , то ректасцензията на Слънцето трябва да е била α1' = 12 h + α1 = 23 h 03 m . В съединение ректасцензията на Слънцето α2' трябва да е същата като ректасцензията на планетата. Следователно за интервала от време от противостоенето до съединението на планетата ректасцензията на Слънцето се е изменила от α1'= 23 h 03 m до α2' = 11 h 59 m . Годишното движение на Слънцето се извършва по посока на нарастване на ректасцензията. Затова то е изимнало по ректасцензия дъга от 12 h 56 m . Това трябва да е станало за интервал от време приблизително 12 h 56 m / 24 h ≈ 0.53889 години. Този интервал е приблизително равен на половината от синодичния период на планетата. Следователно синодичният период е Тsyn = 2 × 0.53889 години = 1.07778 години. За сидеричния период на обикаляне на планетата около Слънцето Тsid можем да напишем:
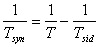
където Т = 1 година е периодът на обикаляне на Земята около Слънцето.

Тsid ≈13.86 години
Полученото число е най-близко до орбиталния период на планетата Юпитер. Разликата между изчисления от нас период и действителния се получава, защото поради наклона на небесния екватор към еклиптиката ректасцензията на Слънцето не се изменя равномерно с времето, и още защото поради променливата скорост на Земята по нейната орбита видимото движение на Слънцето по еклиптиката също не е равномерно.
4 задача.
Недалеч от екватора на Марс е възможно да бъде наблюдавано затъмнение на Деймос от Фобос. Колко време продължава пълната фаза на затъмнението, ако то се случва в зенита на наблюдателя? Приемаме, че орбитите на двата спътника са кръгови и почти лежат в равнината на екватора на планетата.
Справочни данни :
Радиус на Марс 3389.92 km
Период на въртене на Марс 24 h 37 m 22.66 s
Данни за спътниците на Марс
Спътник |
Размер в km
|
Радиус на орбитата в km
|
Сидеричен орбитален период |
Фобос |
22.2 |
9378 |
7 h 39 m 13.84 s |
Деймос |
12.4 |
23459 |
30 h 17 m 54.87 s |
Решение:
Продължителността на затъмението се определя от видимите ъглови размери и видимите ъглови скорости на двата спътника. Видимите ъглови скорости зависят от линейните скорости на спътниците, от разстоянието им до наблюдателя и от линейната скорост на наблюдателя. Когато затъмнението е в зенита, линейните скорости на двата спътника и на наблюдателя са успоредни и са насочени в една посока. Линейната скорост на наблюдателя е
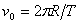 , ,
където R е радиусът на Марс, а Т е периодът му на околоосно въртене. Видимата ъглова скорост на всеки от спътниците е равна на разликата между линейната скорост на наблюдателя и линейната скорост на спътника, разделена на разстоянието от наблюдателя до спътника, т.е. на неговата височина:
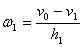
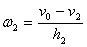
където ω1 и ω2 са видимите ъглови скорости съответно на Фобос и Деймос, v1 и v2 са линейните им скорости, а h1 и h2 са височините им над марсианската повърхност.
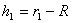
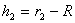
където r1 и r2 са радиусите на орбитите на двата спътника. Ако орбиталните периоди на Фобос и Деймос са Т1 и Т2 , то:
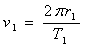
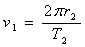
Относителната ъглова скорост на единия спътник спрямо другия е:
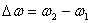
По време на затъмнение Фобос трябва да измине относно Деймос ъглово разстояние:
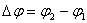
Тук
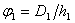 и и 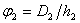 , ,
където D1 и D2 са размерите на Фобос и Деймос. Тогава ако с t означим продължителността на затъмнението:
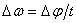
Следоватлено:

t ≈ 11.8 sec
5 задача.
На 28 март 2004 г., три седмици след опозицията на Юпитер, космическият телескоп Хъбъл успя да заснеме рядко явление – затъмнение на Юпитер едновременно от три негови спътника. Разгледайте внимателно снимката. Използвайки схемата на Юпитер и орбитите на Галилеевите спътници, определете коя сянка на кой спътник принадлежи.
На снимката се виждат два от спътниците. Кои са те? Означете техните положения върху орбитите им.
Кой е третият спътник, хвърлящ сянка върху диска на Юпитер? Нарисувайте неговото положение върху орбитата му.

Юпитер на 28 март 2004 г.
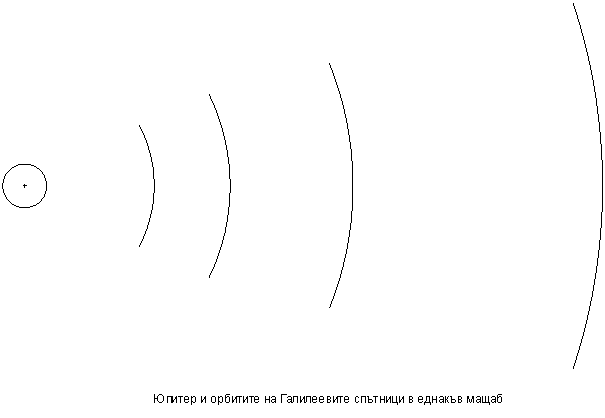
Решение:
Това, че сенките са върху повърхността на Юпитер, означава, че спътниците се намират много близо до линията, свързваща Юпитер и Слънцето. Вижда се, че плоскостта на орбитите на спътниците има лек наклон спрямо направлението Юпитер-Слънце, но това няма да окаже влияние върху решението на задачата. На снимката се виждат две големи сенки и една малка. Измежду Галилеевите спътници на Юпитер два са по-големи – Ганимед и Калисто, и два са по-малки – Йо и Европа. Следователно големите сенки са на Ганимед и Калисто. Ганимед е по-голям от Калисто и е два пъти по-близо до Юпитер. Виждаме, че сянката до левия край на диска е най-голяма и е по-рязко очертана от сянката до десния му край. Затова сянката до левия край на Юпитер е на Ганимед, а до десния му край е на Калисто. На снимката се виждат два от Галилеевите спътници. По-малкият е спътникът, който хвърля малката сянка, а по-големият е спътникът, който хвърля сянката до левия край на диска на планетата, т.е. Ганимед. Забелязваме, че спътниците са стриктно вдясно от сенките, като разстоянията от спътниците до сенките са различни поради различните разстояния на спътниците до планетата. Начертаваме на снимката вертикална линия, перпендикулярна на екватора на планетата и допирателна до левия край на диска на Юпитер. Измерваме разстоянията от нея до центровете на сенките и на дисковете на спътниците в милиметри.
На снимката:
Диаметър на Юпитер 89 mm
Разстояния от вертикалната линия до:
• Сянка на Ганимед – 6 mm
• Диск на Ганимед – 61 mm
• Сянка на малкия спътник – 25 mm
• Диск на малкия спътник – 43.5 mm
• Сянка на Калисто – 72.5 mm
На приложената схема с орбитите измерваме диаметъра на Юпитер: 26 mm . Отношението между диаметрите на Юпитер на схемата и на снимката ни дава коефициент, с който преизчисляваме разстоянията до съответните сенки и спътници за схемата.
• Сянка на Ганимед – 1.8 mm
• Диск на Ганимед – 17.8 mm
• Сянка на малкия спътник – 7.3 mm
• Диск на малкия спътник – 12.7 mm
• Сянка на Калисто – 21.2 mm
На схемата прекарваме две прави линии през центъра на диска на Юпитер. Едната линия АА' е успоредна на картинната плоскост на наблюдателя, другата е перпендикулярна на първата. Пресичайки дъгите на орбитите на спътниците, втората линия сочи направлението към наблюдателя. На схемата ние гледаме Юпитер откъм северния полюс. Линията АА' пресича кръга на планетата там, където е краят на видимия диск на северното полукълбо. Кръгчето на планетата всъщност се очертава от нейния екватор. Затова сенките на Ганимед и Калисто, които са близо до края на диска на Юпитер, ние нанасяме на съответните разстояния от левия край на кръгчето, близо до линията АА'. Сянката на малкия спътник нанасяме близо до линията на екватора, т.е. близо до кръгчето, очертаващо планетата. С две чертички върху линията АА' отбелязваме къде върху картинната плоскост се проектират изображенията на самите спътници, гледани от Земята. Ние вече знаем, че големият спътник е Ганимед. От чертичка (2) прекарваме линия, успоредна на линията към наблюдателя, до пресичането й с орбитата на Ганимед (третата орбита). В тази пресечна точка е положението на Ганимед върху орбитата му. Съединяваме сянката на Ганимед (1) с положението му върху орбитата и получаваме направлението към Слънцето. Това направление е успоредно на слънчевите лъчи. Построяваме линия, успоредна на това направление, от сянката (3) на малкия спътник до пресичането с орбитите на двата близки до Юпитер спътника. След това посторяваме линия, успоредна на направлението към наблюдателя от точка (4), която е проекция на положението на диска на малкия спътник. Виждаме, че двете линии се пресичат върху орбитата на Йо (или близо до нея). Следователно малкият спътник е Йо. Означаваме неговото положение върху орбитата му. Успоредно на линията на слънчевите лъчи построяваме линия от сянката на Калисто (5) до пресичането й с орбитата на Калисто. Получаваме положението на спътника върху орбитата му.

 |