МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА

ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА ПО АСТРОНОМИЯ

ХІІ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ

  Ученици от 7-8 клас

ТЕОРЕТИЧЕН ТУР

Задача 1. Вие членувате в клуб на смелите пътешественици със странни идеи. Решили сте да направите пътуване по суша и море, като се движите само по гринуичкия меридиан. Ориентирате се по звездите. Наблюдавате звездата Феркад (γ Малка мечка) с деклинация  и измервате нейната височина в горна кулминация. Оказва се, че всеки ден височината й е с 1° по-голяма отколкото предния ден. В каква посока се движите? С каква скорост?
На 9 май Феркад се наблюдава в горна кулминация около 0 h по гринуичко време. Приблизително каква е ректасцензията на звездата?

Решение:
Деклинацията на Феркад е  72°. При видимото си движение по небето тя описва денонощния паралел   aa'   с радиус 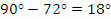 . На различни географски ширини са възможни различни случаи. Може в горна кулминация звездата да е на юг, както е на схема 1). Височината на звездата над хоризонта в горна кулминация се измерва от точката S на хоризонта до a'.

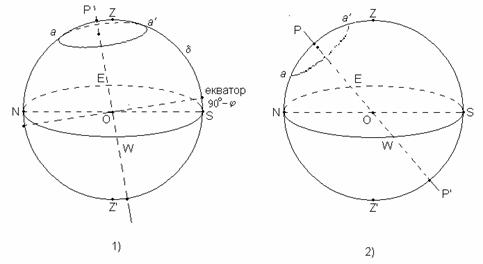
Тогава, ако с всеки следващ ден височината над хоризонта на звездата в горна кулминация е по-голяма, клубът на пътешествениците се движи на юг – вследствие на това северният небесен полюс P се отклонява все повече и повече от зенита за наблюдателя и точката, в която Феркад кулминира, се вдига все по-високо над хоризонта. Това е валидно за географска ширина φ на наблюдателя, за която:
           или                 
Тук δ  е деклинацията на Феркад.
Възможно е, обаче, Феркад да бъде в горна кулминация на север, както ни убеждава схема 2). В този случай височината на звездата над хоризонта в горна кулминация се измерва от точката N на хоризонта до a?. Сега ако пътешествениците наблюдават увеличаване на височината над хоризонта на Феркад в горна кулминация, те се движат на север. Така става, когато . Накрая нека не забравяме, че когато пътешествениците навлязат достатъчно на юг в южното полукълбо, то те няма да виждат Феркад над хоризонта.
Щом височината на звездата се увеличава с 1° на ден, с толкова се променя и географската ширина на пътешествениците. Дължината s на дъга от един градус по земната повърхност можем да изчислим примерно така:

където R е земният радиус. За скоростта на пътешествениците получаваме:

Звездата е в горна кулминация на 9 май в полунощ. Тогава Слънцето е на 180°, или 12h от звездата по ректасцензия. Да намерим ректасцензията на Слънцето. Датата 9 май е определен брой дни след пролетното равноденствие на 21 март:
10 (от март) + 30 (април) + 9 (май) = 49 дни
При пролетното равноденствие Слънцето е имало ректасцензия, равна на 0. На 9 май тя е:

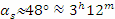
Така за ректасцевзята на звездата получаваме:

Задача 2. Доста често в решенията на задачите, давани от участници в астрономическата олимпиада, се среща следното твърдение: “Слънцето изгрява от изток, а Луната – от запад”. Вярно ли е това твърдение?
Вие сте любители на слънчевите и лунните изгреви. Обичате да ги наблюдавате винаги, когато имате възможност. Всъщност кое от двете явления се случва по-често – изгрев на Слънцето или на Луната?
Обяснете вашите отговори.

Решение:
Изгревът на Луната става при видимото й денонощно движение. То, както и подобни видими движения на други космически тела, се дължи на въртенето на Земята около оста й, което става от запад на изток и затова видимото денонощно движение на небесните светила става в обратната посока – от изток на запад.
Поради това, че Луната изменя своята деклинация в течение на годината, за наблюдатели на различни географски ширини лунният изгрев може да стане както от изток, така и с различни отмествания към североизток и север, или пък югоизток и юг. Но Луната никога не може да изгрява от запад.
Слънцето също изгрява и залязва поради въртенето на Земята около оста й. Така че и то се движи видимо по небето от изток на запад, заедно с Луната. Но Луната обикаля около Земята по своята орбита, като посоката на това значително по-бавно движение е обратна – от запад на изток. За земния наблюдател то се наслагва върху видимото денонощно движение на Луната. Ето защо при видимото си денонощно движение Луната „изостава” от Слънцето. По тази причина лунните изгреви трябва да се случват по-нарядко отколкото слънчевите.
Така е по нашите географски ширини и въобще в обширна област на земното кълбо. Ако обаче сме на един от полюсите, ще се наблюдава нещо доста по-различно. На полюса Слънцето и Луната изгряват не благодарение на видимото си денонощно движение, причинено от околоосното въртене на Земята, а поради движението на Слънцето и Луната на фона на звездите, При Слънцето това движение става по еклиптиката и се дължи на обикалянето на Земята около Слънцето. При Луната движението на фона на звездите става поради нейното обикаляне около Земята. Затова на всеки от земните полюси има само един слънчев изгрев в една година, лунните изгреви стават по веднъж на всеки сидеричен лунен месец от 27.5 дни. Така че, на полюсите лунните изгреви са много по-чести, отколкото слънчевите. Подобна ситуация има и в малка област около северния, както и южния полюси.

Задача 3. Официален наблюдател от Галактичната олимпиада по астрономия гостува на нашата олимпиада в Хасково. Той участва в работата на комисията и предлага задача, свързана с родната му звездна система. Тя е двойна и се намира на разстояние 100 парсека от нас. Едната компонента е звезда, подобна на Слънцето. Другата е червено джудже с маса 4 пъти по-малка от тази на Слънцето и светимост 251.2 пъти по-малка от слънчевата светимост. Орбиталният период на системата е 28.28 земни години.
Бихме ли могли да наблюдаваме двете компоненти на тази система с 2-метровия телескоп в Националната астрономическа обсерватория – Рожен? Пределната звездна величина на телескопа е 16m, а разделителната способност – 1" (дъгова секунда).

Решение:
Ярката звезда в системата е подобна на Слънцето, затова приемаме, че има същата светимост и съответно – същата абсолютна звездна величина 4.7m. Абсолютната звездна величина е звездната величина, която звездата би имала на разстояние 10 парсека от нас. В нашия случай звездата е на 100 парсека, или на 10 пъти по-голямо разстояние. Следователно нейният видим блясък ще намалее 10² = 100 пъти в сравнение с блясъка, който би имала на разстояние 10 парсека. Намаление на блясъка 100 пъти съответства на увеличение на звездната величина с 5m. Така лесно получаваме, че видимата звездна величина на ярката звезда в двойната система е:

Другата звезда в системата има светимост 251.2 пъти по-слаба от главната компонента. Да погледнем внимателно това число: 251.2 = 2.512 х 100. Оттук се вижда, че разликата в звездните величини на компонентите е 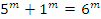. Накрая получаваме, че звездната величина на слабата компонента е:

Тъй като пределната звездна величина при наблюдение с 2-метровия телескоп в Националната астрономическа обсерватория е 16m, с него би трябвало да виждаме слабата компонента.
Нека с М означим масата на главната компонента, а с Т - периодът, с който двете звезди се движат около центъра на масите на системата. Да отбележим, че масата на вторичната компонента е 0.25 М. От ІІІ закон на Кеплер можем да получим оценка за разстоянието r, на което се намират компонентите една от друга:

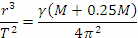
Ако изразяваме r в астрономически единици, Т в години и М в слънчеви маси, можем да напишем:

Дали бихме могли да различим като отделни двете компоненти с телескопа? Разстоянието до двойната система е 100 парсека. Един парсек е разстоянието, от което една астрономическа единица се вижда под ъгъл 1?. От разстояние 100 парсека 10 астрономически единици се виждат под ъгъл 0.1?. Но разделителната способност на нашия телескоп е 1?. Следователно дори и да можем да видим с него звезда с толкова слаб блясък, както блясъка на вторичната компонента, ние не бихме могли да различим тази звезда и по-ярката компонента като отделни звезди.

Справочни данни:
Радиус на Земята        6370 км
Абсолютна звездна величина на Слънцето       4.7m

ПРАКТИЧЕСКИ ТУР

Необикновеното избухване на звездата V838 от Единорог        (V838 Mon).

На 6 януари 2002 г. австралийският астроном любител N. J. Brown преглежда изображения на една област от небето, заснети в различни нощи от неговата патрулна наблюдателна станция за търсене  на нови  звезди.   На една  от  снимките  той  вижда  новопоявил  се  обект  и  събщава в Централното бюро за астрономически телеграми.

Започват се усилени наблюдения на обекта, но изненадващите събития все още предстоят. През февруари само за един ден звездата рязко повишава блясъка си от 11^m до 6.5^m! После блясъкът бавно спада, но в началото на март се наблюдава ново повишение – този път от 9^m до 7.5^m. Оттогва блясъкът на звездата бавно, но стабилно се понижава. Естеството на експлозията все още е загадка за учените. Безспорно става въпрос за последните    стадии   от   живота     на     дълго еволюирала звезда. По някои свои параметри явлението прилича на избухване на нова звезда, но други особености са в противоречие с това предположение. Излъчването от мощния космически взрив преминава през газовата обвивка, изхвърлена от звездата в предните етапи от нейната еволюция. Светлината се разсейва от праховите частици в обвивката и прави видими за нас  все по-отдалечени от звездата части на мъглявината.

Изпозвайте при решението на задачата информацията от тази снимка на областта около V838 с размери 14.6'×9.8'.

Разгледайте следващата поредица от негативни снимки на V838.
• Направете необходимите измервания и постройте графика на изменението на ъгловия диаметър в дъгови секунди на осветената част от мъглявината с времето.
• Приведете аргументи в полза на твърдението, че се наблюдава наистина разпространение на светлинно ехо.
• Оценете разстоянието до V838 Mon.

Решение:
Измерваме с линийка диаметъра на светещата част от мъглявината. Тъй като в нея има много нееднородности, за по-голяма точност можем да направим измервания примерно в две парпендикулярни направления и да усредним резултата. За да получим видимите ъглови диаметри, използваме негативната снимка, дадена в текста на задачата, за която е известен ъгловият мащаб. Измерваме дългата й страна (119 мм) и като знаем, че съответства на 14.6 дъгови минути, намираме:

Сега трябва да приведем мащаба на петте изображения към този мащаб. Измерваме разстоянието примерно между две звезди на снимката с даден ъглов мащаб в близките околности на V838 Mon. После намираме същите тези звезди върху петата снимка от поредицата и измерваме разстоянието между тях на тази снимка. Сравнението показва, че разстоянието между звездите на горната снимка е 0.382 от разстоянието между същите звезди на петата снимка от поредицата.
Сега вече може да превърнем измерените от нас диаметри на последователно увеличаващата се светла част от мъглявината в дъгови секунди:

Построяваме графиката на изменението на диаметъра на светещата част от мъглявината с времето. Виждаме, че се получава линейна зависимост. Това потвърждава предположението, че става въпрос за светлинно ехо, а не за истниско разширение на мъглявината. Правата линия на графиката показва, че диаметърът расте с постоянна скорост, което едва ли би станало при физическо разширение на мъглявината след експлозията на звездата. При такова разширение поради взаимодействието с междузвездната среда скоростта на раздуване на мъглявината би намалявала с времето и графиката на изменение на диаметъра не би била права линия.
На графиката по отрицателната част на оста на времето е нанесена точка, съответстваща на дата на откриването на явлението – 6 януари 2002 г.

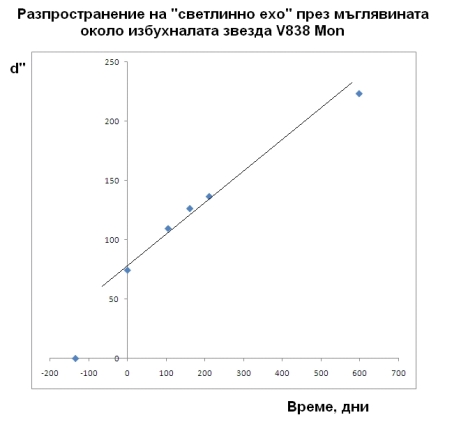От момента на първата снимка в поредицата до момента на петата снимка светлината се е разпространявала в течение на 598 дни, или 598/365.25 ≈1.64 години. Така светлината е изминала разстояние 1.64 светлинни години. Но взривът е станал в центъра на мъглявината значително време преди това. От графиката става ясно, че е било преди първото откритие на явлението, т.е. – 6 януари 2002 г. Ако приемем приблизително, че взривът е станал на тази дата, то светлината се е разпространявала 2 години – изминала е 2 светлинни години от началото до момента на последната снимка и това съответства на радиуса на мъглявината. Следователно диаметърът на мъглявината е 4 светлинни години. Оттук вече можем да пресметнем разстоянието до мъглявината: