МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА

ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА ПО АСТРОНОМИЯ

ХІІ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ

  Ученици от 11-12 клас

ТЕОРЕТИЧЕН ТУР

Задача 1. Прословутите палавници Макс и Мориц са станали космонавти, но след многобройни поразии са изхврълени от командира на кораба в открития космос далеч от планети и звезди. Всеки от тях заедно със скафандъра си тежи 200 кг. Намират се на 20 м един от друг и обикалят по кръгови орбити около общия си център на масите.
Намерете орбиталния им период и техните скорости относно центъра на масите.
Макс и Мориц искат да се приближат един към друг, за да потърсят начин за спасение. В джоба на скафандъра си Мориц държи 200-грамов кристален мозък, отмъкнат от един от бордовите компютри, който също може да им помогне в мисленето. По какъв начин двамата космонавти могат да се сближат? За колко време може да стане това?

Решение:
Орбиталния период намираме от ІІІ закон на Кеплер:

=

Където  r  e разстоянието между двамата космонавти, m  е масата на всеки от тях, а  γ е гравитационната константа.

 денонощия

Скоростта на всеки от тях относно центъра на масите е:

 mm/sec

Единственият начин космонавтите да се сближат, е да използват закона за запазване на импулса. Един от тях трябва да си придаде скорост, равна по големина и насочена обратно на относителната си скорост спрямо другия, т.е. 2v. Така движението им един относно друг ще спре и те ще започнат да падат един към друг под действие на гравитацията си. За да си придаде неоходимата скорост единият космонавт трябва да жертва нещо от себе си и даго хвърли по посока на движението си. Така че, ще им се наложи да жертват кристалния компютърен мозък. Да означим неговата маса с m₁ . Скоростта u , с която той трябва да бъде хвърлен, се определя от равенството:

mm/sec

За да намерим времето на сближаване на космонавтите, приемаме, че единият от тях се движи по безкрайно сплесната елипса с фокус в другия космонавт и голяма полуос половината от разстоянието между тях. От ІІІ закон на Кеплер намираме орбиталнния период и времето за падане е половината от този период:

 денонощия

Задача 2. Вие сте придворен астроном при велик марсиански владетел. Наблюдавате спътниците Фобос и Деймос с цел да усъвършенствате марсианската календарна система.
В каква посока ще става видимото денонощно движение на Фобос и Деймос по марсианското небе?
За времето между два изгрева на Деймос колко изгрева на Фобос ще се наблюдават?
Да предположим, че в някакъв момент наблюдател на марсианския екватор вижда окултация на Деймос от Фобос. В какъв интервал от време около този момент ще съществуват точки от повърхността на Марс, от които  също ще може да се види окултация на Фобос и Деймос? Приемаме, че орбитите на двата спътника лежат в екваториалната равнина на Марс.

Решение:
Двата спътника на Марс се движат около планетата в същата посока, в която става и околоосното й въртене. Веднага виждаме, че орбиталният период да Фобос T_F е по-кратък от периода на околоосно въртене на Марс T_M . Това означава, че за наблюдател на марсианската повърхност Фобос ще изгрява от запад и ще залязва на изток. Орбиталният период на Деймос T_D е по-дълъг от T_M , така че Деймос ще изгрява от изток и ще залязва на запад. Нека времената между два изгрева на Фобос и на Деймос са съответно T_F’ и T_D’. В сила са следните съотношения:

От тях получаваме:

 денонощия
 денонощия

Получава се, че за времето между два изгрева на Деймос Фобос може да изгрее 11 пъти!

Нека в даден момент за наблюдател на марсианския екватор се вижда окултация на Деймос от Фобос, която е в зенита. В някакви моменти от време малко преди или малко след този момент от съседни точки на повърхността на Марс също могат да се виждат такива окултации. Точките са ограничени върху дъгата A’A”. Нека разглеждаме ситуацията в координатна система, която се върти около центъра на Марс заедно с Деймос. Интервалът от време, който търсим е равен на интервала от време, за който Фобос изминава дъгата B’B” от своята орбита в тази координатна система, или с други думи, като се движи с ъглова скорост, съответстваща на синодичния му период спрямо Деймос:

 денонощия

Нека  r_F  и  r_D  са радиусите на орбитите на Фобос и Деймос, а  R_M  е радиусът на Марс. За ъглите α и β получаваме:

Дъгата В’B” съответства на ъгъл . Тя ще сеизмине от Фобос за време:

В този времеви интервал ще могат да се наблюдават окултации на Деймос от Фобос.

Задача 3. В последно време астрономите откриват множество планети около други звезди. В сравнение с планетите от родната ни Слънчева система, преобладаващата част от тези далечни планети са твърде необикновени. Една такава планета е открита около звездата WASP 4. Звездата е от спектрален клас G7, с температура 5500 К и радиус 1.15 слънчеви радиуса. Намира се на 300 парсека от нас. Планетата е с маса 1.12 пъти по-голяма от масата на Юпитер и обикаля около звездата на разстояние само 0.023 астрономически единици с период 1.3382 земни денонощия.

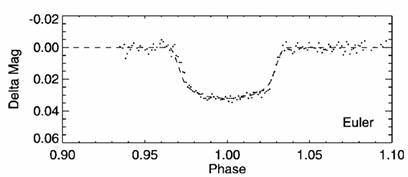
Графиката показва изменението на блясъка на звездата по време на наблюдаван пасаж на планетата по диска на звездата. Използвайте данните от графиката и определете радиуса на планетата. Направете това по два начина и сравнете получените от вас резултати. Коментирайте разликите.
При пасажа планетата преминава приблизително през центъра на видимия диск на звездата. По вертикалната скала е нанесена не самата видима звездна величина на звездата, а нейното изменение спрямо стойността, която има извън времето на пасажа.

Решение: Намаляването на блясъка на звездата се дължи на това, че планетата застава между нея и наблюдателя като засенчва част от светлината. Когато планетата не е пред звездата, осветеността Eo , която звездата създава на Земята, е пропорционална на  πR_зв² , където R_зв е радиусът на звездата:

Е_o ~ πR_зв²

Когато планетата е пред звездата светлина идва само от тази част от звездата, която не е засенчена от диска на планетата:

Е₁ ~ π( R_зв² – R_пл² )

От формулата на Погсон:

Е_o / Е₁ = 2.512^Δm

R_зв²/ (R_зв² – R_пл²) = 2.512^Δm

R_пл =  R_зв (1 – 1/2.512^Δm )^1/2

Измерваме амплитудата на изменение на блясъка и получаваме:      Δm = 0.032^m

Пресмятаме и получаваме за R_пл:   R_пл =  0.17R_зв≈ 140000 km    

Вторият начин за определяне на размерите на звездата е свързан с геометрията на затъмнението. Затъмнението започва, когато дискът на планетата започне да засенчва диска на звездата. Максимална фаза настъпва, когато целият диск на планетата застане пред диска на звездата. Следва плосък минимум докато дискът на планетата не достигне срещуположния край на диска на звездата. Следва край на затъмнението в обратен ред. В пълна фаза обикновенно се наблюдава известна заобленост на минимума. Тя се дължи на потъмнението към края на  диска на звездата. Основните моменти на затъмнението схематично са показани на фигурата.

Ширината  в горната част на минимума е равна на:

L₁ =  2(R_зв +  R_пл)

Ширината в долната част на минимума плюс интервалът на покачване на блясъка е:

L₂ = 2R_зв

Делим първия израз на втория и получаваме:

L₁/L₂ = 1 +  R_пл /R_зв

R_пл =  (L₁/L₂ – 1 )R_зв  =  0.17R_зв ≈ 140000 km    

Виждаме, че двата метода водят до еднакви или близки резултати.

Справочни данни:
Радиус на Земята  6370 км; 
Радиус на Слънцето  700000 км      
Орбитален период на Фобос – 0.31891 земни денонощия
Орбитален период на Деймос – 1.26244 земни денонощия
Период на околоосно въртене на Марс – 1.02595 земни денонощия

ПРАКТИЧЕСКИ ТУР

Юпитер и Ганимед

От наземни наблюдения на Юпитер е определено, че екваториалният му радиус е 71495 km, а радиусът на орбитата на Ганимед е  1070000 km. На 19 януари 2005 година, десетина дни след една западна квадратура на Юпитер, с космическият телескоп в продължение на около половин час са получени серия изображения на Ганимед и части от диска на планетата. Изображенията са правени в различни филтри и върху тях е посочено и времето в UT с точност до минута. Използвайте първите две, по време, изображения за определяне на диаметъра на Ганимед, а по изображенията с началото на окултацията на спътника определете масата на Юпитер.

Решение: Виждаме, че с напредване на времето Ганимед се приближава към диска на Юпитер и след това започва да се скрива зад него. Тъй като Ганимед има право движение, то той се приближава към западната половина на диска на планетата. Следователно на първите две изображения се вижда западната и южната част на диска на Юпитер.
Диаметъра на Ганимед можем да определим като го сравним с екваториалния радиус на Юпитер. Построяваме една или няколоко прави успоредни на системата ивици  по повърхността на Юпитер, които са успоредни на видимия екватор на планетата. Построяваме права, перпендикулярна на тях и допирателна към западния край на диска на планетата, където е и западния край на видимия екватор на диска на Юпитер. Построяваме права успоредна на ивиците и допирателна към южния край на диска на Юпитер. Точката на допиране е почти в Южния полюс на планетата поради пренебрежимо малкия наклон на оста на Юпитер. Отсечката от Южния полюс до точката на пресичане на правата с допирателната към западния край на диска е равна на екваториалния радиус на планетата. Измерваме с линийка и получаваме  R_Ю = 68 мм. Делим истинския размер на екваториалния радиус на измерената стойност и получаваме, че мащабът на изображението е  1051.4 км   на милиметър.
Измерваме диаметъра на Ганимед в милиметри и получаваме  D_Г = 5 мм. Умножаваме по мащаба и получаваме за истинския  диаметър на Ганимед  D_Г = 5257 км.
Да преминем към изображенията със скриването на диска на Ганимед зад Юпитер. За да определим масата на Юпитер трябва да определим скоростта на движение на Ганимед по орбитата му. При наблюдаваното скриване на Ганимед зад Юпитер, той се намира в най-далечната част на орбитата си и се движи перпендикулярно на лъча на зрение на наблюдателя. Това е така, защото радиусът на орбитата на Ганимед е съществено по-голям от радиуса на Юпитер. От друга страна Юпитер е наблюдаван след квадратура и следователно е недалеч от точката на стоене. В тази точка той видимо не се движи спрямо звездите, а близо до нея се движи спрямо тях много бавно. Пребрегваме това движение, имайки предвид неголямата точност на графичните построения и измервания. Тогава наблюдаваното движение на Ганимед спрямо Юпитер ще представлява сидерично движение и измерената скорост ще бъде сидеричната скорост на Ганимед по неговата  орбита. Точно тази скорост ни е необходима за пресмятане на масата на Юпитер.
Равнините на орбитите на Галилеевите спътници лежат почти точно в равнината на екватора на Юпитер. Следователно видимото движение на Ганимед става по права успоредна на екватора на планетата. Тази права е наклонена към рамките на изображенията на същия ъгъл както и на първите две изображения. Измерваме или пресмятаме ъгъла (от някой правоъгълен триъгълник) и получаваме за ъгъла на наклона на екватора към хоризонталната рамка  α = 40°.5 .  Скриването на западната точка на диска на Ганимед зад края на диска на Юпитер става точно там, където става и скриването  на източната точка от диска на Ганимед. Ние, обаче, не  можем да използваме тези моменти. От една страна е почти невъзможно да се проследят тези точки от изображение към изображение. От друга страна е съвършенно невъзможно да се идентифицира и проследи съответната точка от диска на Юпитер. Това което можем да измерим е скоростта на потапяне на Ганимед зад диска на Юпитер. Измерваме диаметъра на видимия на изображенията диск на Ганимед и получаваме  D_2Г = 11 мм.  Измерваме височината на частта  Dx  от диска на Ганимед, която остава, все още, над края на диска на Юпитер. Използваме шест от изображенията, от второ до седмо (от 22:11 UT  до 22:19 UT). При тях е възможно да се направят достатъчно прецизни измервания. Построяваме графика на зависимостта на  Dx от времето. Виждаме, че тя е леко извита. Това се дължи на това, че във всеки момент от време най-високата точка от диска на Ганимед се намира над все по южна точка от края на диска на Юпитер. Една от точките не лежи на кривата (от  22:16 UT).  Вероятно причината е в това, че изображението е правено в близката инфрачервена област – 892 nm. Намираме средният наклон на кривата като използваме първата и последната точки. Виждаме, че за 8 минути се скриват 6.9 мм от диска на Ганимед.
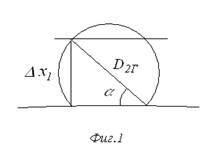
От Фиг.1 се вижда, че е достатъчно да определим времето за което се потапя частта Δx₁ от диска на Ганимед. Тази част е :  

Δx₁= D_2Г · sin α = 7.14 мм.

Времето за което тази част се скрива е:

 t₁= (8/6.9)Δx₁ min = 8.28 min = 8m17s .

Това е времето за което Ганимед изминава един свой диаметър по орбитата си.  Скоростта с която той се движи е:

v = D_2Г / t₁  =  10.58  km/s .

Орбитата на Ганимед е почти кръгова. Тогава от формулата за първа космическа скорост получаваме:

M_Ю = v². r / γ  ≈  1.8×10²⁷ kg

Истинската маса на Юпитер е    1.9×10²⁷ kg .   Виждаме, че с  елементарни измервания и пресмятания може да получим много добра оценка за масата на Юпитер.