МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА

ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА ПО АСТРОНОМИЯ

ХІІ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ

  Ученици от 11-12 клас

1 задача. Звезди. Както знаем, поради видимото денонощно въртене на небесната сфера, звездите променят своето положение спрямо хоризонта и посоките на света. Има звезди, които изгряват и залязват, има звезди, които са незалязващи и такива, които са неизгряващи. Дали има места по земната повърхност, откъдето едни и същи звезди в горна и долна кулминация са на еднакво ъглово отстояние от хоризоната? Къде са тези места? Какви звезди биха отговаряли на тези условия? Има ли такива звезди?
При решаването на задачата не отчитайте рефракцията.
           
Решение:
Нека пренебрегнем собственото движение на звездите.
Кулминация на звезда е преминаването й през меридиана на мястото. Кулминацията, при която звездата е на по-голяма височина над хоризонта, наричаме „горна“, другата кулминация наричаме „долна“. Долната кулминация може да се случи и под хоризонта на наблюдателя.
Да разгледаме двата характерни случая – звезда гледана от екватора и от полюса, и общия случай – звезда гледана от място с междинна географска ширина.
На екватора всички звезди са изгряващи и залязващи. Ако не отчитаме рефракцията, полюсите лежат на хоризонта а звездите се движат по малки кръгове, които са наполовина над хоризонта и нополовина – под него. Очевидно е, че в горна и долна кулминация звездите ше бъдат на едно и също ъглово разстояние от хоризонта  h = 90 - d, където d е деклинацията на звездата. Ако звездата е на небесния екватор, то в горна кулминация тя ще преминава през зенита, а в долна – през надира. Ако звездата е на някой от небесните полюси, то тя и в горна и в долна кулминация ще се намира на хоризонта. Следователно, когато сме на екватора на Земята, всички звезди ще са на едно и също ъглово разстояние от хоризонта в горна и долна кулминация.
На полюсите на Земята звездите се движат успоредно на хоризонта. Тук не може да се дефинира понятието меридиан на мястото и следователно не може да се определи момент на кулминация на звездите. Бихме могли да кажем, че за  полюсите въпросът е безсмислен. Но, при голямо желание, бихме могли и да приемем, че всички звезди по всяко време са и в горна и в долна  кулминация (т.е. всеки меридиан е меридиан на мястото) и условието е изпълнено за всички звезди, при това във всеки един момент от време.
Ако не сме на екватора или полюса има само един денонощен паралел, за който се изпълнява исканото условие. Този паралел съвпада с небесния екватор. Само ако звездата се намира на небесния екватор, тя ще е на едно и също ъглово разстояние от хоризонта в горна и долна кулминация. В горна кулминация звездата ще е над хоризонта, а в долна – под хоризонта. Разбира се, ако звездата е точно в небесния полюс, горната и долна кулминации съвпадат и условието е изпълнено.
Съществуват ли звезди, които изпълняват поставените условия?
За първия случай, когато сме на екватора, това са всички звезди на небето.
За случая на полюса, както видяхме, има две възможности – или няма нито една звезда, ако приемем, че необходимите понятия не могат да бъдат дефинирани, или, във втория случай, това отново са всички звезди на небето.
За случая на междинна географска ширина въпросът е много по-сложен.
Нека приемем, че звездите са точкови обекти, т.е. ъгловите им размери са нула. За да е изпълнено условието за равенство на ъглите звездата трябва да е на небесния екватор. При това трябва да е съвсем точно на небесния екватор. Тъй като звездите са точки, разположени в значителна степен случайно по повърхнина, макар и въображаема (небесната сфера), то вероятността някоя звезда да попадне на точно определена линия (небесния екватор) е практически нула. Ако, обаче, приемем че звездите имат крайни, макар и малки, ъглови размери и приемем, че една звезда е на екватора когато той пресича нейния диск, то тогава вероятността да има звезди на екватора е различна от нула, дори и да е много малка.
Същото се отнасят и за случая на звезда точно на небесния полюс.
Всички досегашни разсъждения са направени при едно съществено приближение. Ние негласно приехме, че оста на Земята е неподвижна, т.е. че  тя не променя своята ориентация в пространството. Това, обаче, не е така. Поради гравитационното влияние на Луната и Слънцето и поради това, че формата на Земята не е идеално сферична, земната ос прецесира с период около 26000 години, като описва в пространството конус (в първо приближение) с ъгъл при върха 47°  и ос насочена към полюса на еклиптиката. Прецесията води до непрекъсната промяна на ориентацията в пространството на небесната ос, на небесния екватор и следователно на моментните координати на звездите и в частност на деклинацията.  Дали прецесията премахва всяка възможност условието да бъде изпълнено? Това не е съвсем така. В близост до големия кръг, който минава през еклиптичните полюси и равноденствените точки, деклинацията практически не се променя вследствие на прецесията. В определени моменти от време звезди ще попадат на място, до този голям кръг, в което тяхната деклинация в една горна кулминация ще е точно равна на деклинацията им в следваща долна кулминация. Това ще е вярно само за съответната звезда в точно определен момент от време и следователно за точно определена географска дължина на земната повърхност. Това ще е вярно за съответната точка от екватора както и за полюса. За междинни географски ширини условието ще се изпълни само ако звездата, и в двата момента от време, се намира на небесния екватор. Ако отчетем и прецесията на еклиптиката, т.е. отчетем това, че „окръжността“, която северният небесен полюс описва по небесната сфера, не е затворена, а е по-скоро спирала, то разсъжденията ни от предходния абзац пак ще са верни. Единствено ще се промени, много малко, положението на звездата до разглеждания голям кръг, минаващ през точките на слънцестоене. Двете положения, отговарящи на кулминациите на звездата, вече няма да са симетрично разположени относно големия кръг (за централен момент от време), а ще са леко преместени в една от посоките така, че да се компенсира промяната на деклинацията вследствие на прецесията на еклиптиката.

2 задача. RZ Cassiopeiae. Затъмнително двойната звезда RZ Cassiopeiae представлява система, която се състои от две звезди, обикалящи около общия си център на масите.  Орбиталната им равнина е разположена спрямо нас така, че звездите периодично се закриват една друга. Затова в кривата на блясъка на RZ Cas има редуващи се главни и вторични минимуми.

Следващата таблица съдържа данни за двете компоненти на системата RZ Cas.

• Пресметнете амплитудата на изменение на звездната величина на променливата звезда. Считайте, че затъмнението на едната компонента от другата е централно.
• Как бихте обосновали твърдението, че в процеса на еволюцията на системата вещество от едната компонента изтича към другата?

Решение:
От данните можем да изчислим светимостите на двете компоненти:
                               
където Т_А и Т_В са температурите на двете компоненти, R_A и R_B са техните радиуси, а σ е константата на Стефан-Болцман. Данните показват, че по-слабата компонента е В. Когато блясъкът на променливата звезда е максимален, ние виждаме светлина и от двете компоненти – те не се закриват една друга. Следователно осветеността  E_max , създадена от двойната звезда тогава, е пропорционална на  . При главен минимум получаваме светлина само от по-слабата компонента В и осветеността E_min , създавана в такъв случай е пропорционална на  L_B . По-нататък пресмятаме:

Амплитудата на изменение на звездната величина  Δm  намираме чрез формулата на Погсон:

Компонентите от двойната система са се формирали приблизително по едно и също време. Следователно те са практически на еднаква възраст, що се отнася за периода от време, през който са съществували от образуването си досега. Както знаем, обаче, звездите с по-големи маси преминават по-бързо през различните стадии на еволюция. Параметрите на компонентата А показват, че тя все още се намира на Главната последователност върху диаграмата на Херцшпрунг-Ръсел. Но компонентата В е твърде необикновена. Понеже е с по-малка маса от А, тя трябва да е по-хладна и наистина температурата й е значително по-ниска. Бихме сметнали, че и тя е обикновена звезда от Главната последователност, близка до червените джуджета. Но озадачаващото е, че тя има по-голям радиус от А. Всъщност някога в системата RZ Cas компонентата В е била по-масивната, по-горещата и по-ярката. Тя първа е започнала да излиза от главната последователност и да става червен гигант – атмосферата й е започнала да се раздува и температурата й да се понижава. Когато се е раздула достатъчно, вещество от нея е започнало да изтича към компонентата А. Постепенно компонентата В е изгубила значителна част от своята маса и светимостта й е станала по-ниска от тази на А. Така можем да обосновем твърдението, че има изтичане на вещество от едната компонента към другата.

3 задача. Снаряд към Луната. В своя роман “Пътешествие към Луната” Жул Верн описва изстрелването на снаряд от огромно оръдие, вкопано в недрата на планината. Снарядът се изстрелва от екватора така, че да лети радиално от Земята.
• С какава скорост трябва да се изстреля снарядът, така че да достигне до лунната орбита? Не отчитайте съпротивлението на земната атмосфера и гравитационното влияние на Луната върху снаряда.
• Оценете приблизително времето, за което снарядът ще достигне до лунната орбита.
• Отговорете само качествено с какви фактори трябва да се съобрази моментът на изстрелването на снаряда, така че наистина да стигне до Луната.
Разстоянието Земя-Луна е 384 000 км. Масата на Земята е  кг, а радиусът 6370 км, гравитационната константа е  м³кг^-1сек^-2.

Решение:
Необходимата начална скорост  v₀  на снаряда можем да намерим чрез закона за запазване на енергията. Пълната механична енергия на снаряда в момента на откъсването от земната повърхност е:

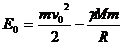
където  m  е масата на снаряда,  M  и R са масата и радиусът на Земята,  а γ е гравитационната константа. Ако снарядът лети радиално от Земята, то при достигане до лунната орбита скоростта му трябва да стане нула. В този момент енергията на снаряда е:

където  r  е радиусът на лунната орбита. Съгласно закона за запазване на енергията, , откъдето намираме:

km/sec

Както виждаме, получава се стойност, доста близка до втора космическа скорост за Земята, но в това няма нищо изненадващо, след като условието е корабът да достигне до разстояние от Земята около 60 пъти по-голямо от нейния радиус.
Ако решим да отчетем околоосното въртене на Земята, то трябва да отбележим, че за да се движи радиално от нашата планета, снарядът трябва да се изстреля през тунел, който не е точно вертикален, а с лек наклон, и началната скорост на снаряда, освен вертикалната компонента v₀,  трябва да има компонента, противоположна на линейната скорост на въртене на точката от земната повърхност, от която той излита.
Времето за достигане на снаряда до лунната орбита можем приблизително да оценим, като приемем, че  и представим движението на снаряда като орбитално движение около Земята по много силно сплесната елипса с голяма полуос, равна на  r/2. Периодът  T  на такова орбитално движение намираме от ІІІ закон на Кеплер:

Търсеното време t , за което снарядът ще дстигне до лунната орбита, е равно на половината от този период, или:

 часа ≈ 4.8 дни ≈ 4 дни 20 часа

При изстрелването си от Земята снарядът се движи радиално от нея и достига лунната орбита в точка А след време 4.8 дни. Тогава и Луната трябва да бъде в същата точка. Луната се движи по своята орбита от запад на изток с период 27.3 денонощия. Денят на изстрелването на снаряда трябва да се избере така, че в него Луната да е отклонена на подходящия ъгъл по своята орбита на запад от точка А и да може да измине този ъгъл за 4.8 дни. Часът на изстрелването трябва да се избере така, че при околосното си въртене Земята да застане в положение, при което точка А е в зенита за пункта, от който се изстрелва снарядът. Съобразно с това трябва да се избере и мястото на изстрелване на снаряда.

4 задача. Смяна на сезоните. Земята обикаля около Слънцето по елиптична орбита с голяма полуос км. В перихелия на земната орбита разстоянието Земя-Слънце е приблизително с км по-малко, а в афелия –с км по-голямо от тази стойност.
Според съвременните представи за формирането на климата на Земята, най-голямо значение има слънчевото греене, т.е. количеството слънчева енергия, падащо върху единица площ, на различни географски ширини. Имайки предвид това, коментирайте влиянието на елиптичността на земната орбита и на наклона на земната ос спрямо еклиптиката върху смяната на годишните времена на нашата планета. Подкрепете разсъжденията си с пресмятания.
Наклон на земната ос спрямо перпендикуляра към равнината на еклиптиката – 23°.5

Решение:
Нека вземем участък от земната повърхност, за който Слънцето е в зенита – слънчевите лъчи падат вертикално. Можем да сравним осветеността  E_p , създавана от Слънцето на такъв участък, когато Земята е в перихелий, и осветеността E_a , когато Земята е в афелий. Означаваме с  km средното разстояние Земя-Слънце и с  km разликата между средното разстояние и разстоянията в перихелий и афелий. Осветеността е обратно пропорционална на квадрата на разстоянието до светлинния източник:
                                 
Отношението на двете осветености е:

С други думи осветеността на земната повърхност в перихелий е с около 7% по-висока, отколкото в афелий.
За да оценим влиянието на наклона на земната ос, нека разгледаме осветеността по пладне в деня на лятното слънцестоене и в деня на зимното слънцестоене за точка, намираща се в умерения пояс, например на 45° географска ширина. Избираме този пояс, тъй като в него има по-големи сезонни изменения. За 45° географска ширина височината на Слънцето над хоризонта по пладне в деня на лятното слънцестоене е , а при зимното слънцестоене . Тук е наклонът на земната ос спрямо оста на еклиптиката. Да означим осветеностите, които създава Слънцето по пладне в дните на лятното и на зимното слънцестоене с  E₁ и   E₂ . Ъглите на падане на слънчевите лъчи спрямо вертикалата към земната повърхност в двата случая ще са съответно   и  . Нека   E₀  е осветеността, която би създавало Слънцето при равни други условия, ако лъчите му падаха перпендикулярно на земната повърхност. Тогава можем да напишем:
                          
Отношението на двете светимости е:

Осветеностите се различават 2.5 пъти! Като сравним това със седемте процента разлика, която се получава поради елиптиччността на земната орбита, можем да заключим, че определящо за смяната на годишните времена на Земята е влиянието на наклона на земната ос.

5 задача. Венера. Орбиталният период на движение на Венера около Слънцето е 224.7 денонощия. Венера е забележителна с това, че се върти около оста си обратно на посоката на орбиталното си движение около Слънцето. Както е известно, приливното въздействие на Земята е оказало влияние върху околоосното въртене на Венера. Затова сега винаги при долно съединение Венера е обърната с една и съща своя страна към Земята.
• Въз основа на тези данни пресметнете периода на околоосно въртене на Венера (звездно денонощие), като имате предвид, че той е по-дълъг от една венерианска година и по-кратък от една земна година.
• Пресметнете продължителността на слънчевото денонощие за Венера.  

Решение:
Нека в даден момент Земята и Венера са в положение 1 на схемата и Венера е в долно съединение. Точката А се намира около центъра на обърнатата към Земята страна на Венера. Нека следващото долно съединение се случва, когато Земята и Венера се намират в положение 2.

Интервалът от време между тези два момента е равен на синодичния период на Венера. Означаваме дадения ни орбитален период на Венера, който е сидеричният й период, с денонощия, а с денонощия – орбиталния период на Земята. Пресмятаме синодичния период на Венера  T_SYN  от формулата:

 денонощия

За този период от време Земята е направила една обиколка около Слънцето и част от следващата обиколка в продължение на  дни. За това време Земята е изминала ъгъл от своята орбита:

За целия синодичен период на Венера T_SYN  планетата се е завъртяла около оста си така, че в положение 2 тя отново е обърната към Земята със същата си страна. Това се вижда от положението на точка А на схемата при второто долно съединение на Венера. Да намерим ъгъла β₁ , на който се е завъртяла около оста си Венера за това време. Тя се върти около оста си обратно на движението си по орбитата. Както можем да се убедим от схемата,  , където . Нека приемем, че . Тогава за време  денонощия Венера трябва да се е завъртяла на ъгъл  около оста си, което означава, че периодът й на околоосно въртене е по-голям от 583.93 денонощия. Но по условие този период е по-кратък от една земна година. Да разгледаме случая, когато  . Тогава . Периода на околоосно въртене на Венера намираме от съотношението:

                                (1)

 денонощия

Отново получаваме период по-голям от една година. Нека сега , при което 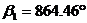. Отново използваме формула (1), за да пресметнем периода:

денонощия

Най-после получаваме стойност, която отговаря на условието да е по-голяма от една венерианска година и по-малка от една земна година. Лесно можем да проверим, че при по-големи стойности на n вече ще се получат периоди по-малки от една венерианска година. Следователно единственото решение е, че периодът на околоосно въртене на Венера е около 243 денонощия, което отговаря и на действителната стойност.
Слънчевото денонощие на Венера  P’  можем да намерим по формулата:

в която знакът „+” фигурира поради това, че околоосното въртене на Венера е в обратна посока на орбиталното й движение около Слънцето.

 дни

През такъв период от време се сменят денят и нощта на Венера.