МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА

ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА ПО АСТРОНОМИЯ

ХІ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ

  Ученици от 7-8 клас

1 задача.
• Може ли да се види Луната на дневното небе?
Ако считате, че е възможно, опитайте се да откриете Луната на небето през деня. Запишете датата и часа на наблюдението. Нарисувайте как изглежда Луната.
Ако считате, че не е възможно, обяснете защо.
• Луната обикаля около Земята от запад на изток. Откъде изгрява Луната – от западната или от източната част на хоризонта? Обяснете своя отговор.

Решение:

Луната обикаля около Земята от запад на изток. При различните взаимни разположения на Луната със Земята и Слънцето, за нас, земните жители, тя показва различни фази. В същата посока, от запад на изток, става и въртенето на Земята около нейната ос. През деня небето е светло, защото земният въздух разсейва слънчевите лъчи. Поради яркостта на дневното небе ние не можем да видим на него звездите (поне не с невъоръжено око). Но яркостта на осветената от Слънцето част на Луната е по-голяма. Затова Луната може да се вижда на дневното небе, макар и не винаги.

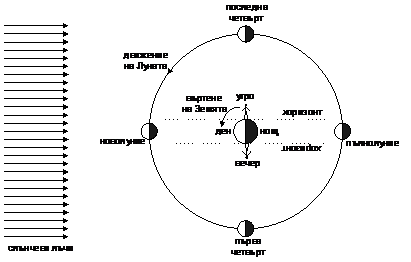
От фигурата става ясно, че Луната трудно може да се види през деня във времето около пълнолуние. Тогава тя се скрива под хоризонта сутрин, малко преди изгрева на Слънцето и изгрява вечер, малко след залеза му. Поради рефракцията е възможно, обаче, дори и при пълнолуние да се виждат едновременно в две противоположни посоки на хоризонта и Слънцето, и Луната. По-трудно е да се види Луната около и в момента на новолуние. Тогава тя е обърната към нас главно с тъмната си, неосветена от Слънцето страна. По принцип тогава Луната би трябвало да се вижда като много тънък сърп, но поради малкото си видимо ъглово отстояние от Слънцето, тя се губи в неговите лъчи. При всички други свои фази Луната може да се види на дневното небе. Около първа четвърт тя се вижда над хоризонта през втората половина от деня, а около последна четвърт – през първата половина от деня.
Както вече беше отбелязано, Луната се движи по своята орбита около Земята от запад на изток. Това става с период около 27.3 денонощия Ако Земята не се въртеше около своята ос, щяхме да наблюдаваме Луната да изгрява от западната част на хоризонта и да залязва към източната част. Но Земята се върти около оста си, при това с много по-кратък период – едно денонощие. Тъй като въртенето на Земята също става от запад на изток, то ние наблюдаваме видимо денонощно движение на звездното небе от изток на запад. В него участва и Луната. В сравнение с видимото движение на звездите тя се движи малко по-бавно, или “изостава” от тях, поради орбиталното си движение около Земята. Но в крайна сметка наблюдаваното от Земята видимо денонощно движение на Луната става от изток на запад – тя изгрява от източната част на хоризонта и залязва към западната част.

2 задача. Няма нищо по-бързо от светлината. Нейната скорост е 300 000 километра в секунда. Но разстоянията между космическите обекти са огромни. Затова ние виждаме космическите обекти не такива, каквито са сега, а каквито са били преди известно време – времето, необходимо на тяхната светлина, за да стигне до нас.
• Какво е разстоянието от Земята до Слънцето? За колко време светлината от Слънцето стига до нас?
• Като единица мярка за разстоянията между звездите се използва светлинната година. Една светлинна година е равна на разстоянието, което светлината изминава за една година. Пресметнете колко километра има в една светлинна година.
• Напишете това число с думи (словом).
• Разстоянието от Слънцето до най-близката звезда Проксима е 4.3 светлинни години. Колко пъти то е по-голямо от разстоянието между Земята и Слънцето?

Решение:

Разстоянието от Земята до Слънцето е 150 000 000 километра. Светлината достига от Слънцето до нас за време:

секунди, или
минути

Когато погледнем към Слънцето, ние го виждаме такова, каквото е било преди 8 минути.
В една светлинна година има:
300 000 km/s × 60 s × 60 min × 24 ч. × 365.25 денонощия ≈ 9 467 280 000 000 km
С думи това число се записва така: девет трилиона четиристотин шестдесет и седем милиарда двеста и осемдесет милиона километра. Нека обърнем внимание още веднъж, че светлинната година не е мярка за време, а за разстояние.
Като знаем на колко километра е равна една светлинна година, можем да пресметнем разстоянието до най-близката звезда Проксима. То е:
4.3 св. г. × 9467280000000 km = 40 709 304 000 000 km
За да разберем колко пъти то е по-голямо от разстоянието до Слънцето, пресмятаме:
40 709 304 000 000 km : 150 000 000 km ≈ 270 000 пъти!
Разстоянията между звездите са наистина огромни.

3 задача. Разделителната способност на космическия телескоп Хъбъл (Hubble Space Telescope) е около 0.1″ (дъгови секунди). Това е най-малкото видимо ъглово отстояние мeжду две звезди, при което те биха могли да се различат като отделни звезди с телескопа.
• На какво разстояние от вас трябва да застане ваш приятел, за да го виждате под такъв ъгъл? При пресмятанията посочете ръста на вашия приятел.
• Определете разделителната способност на вашите очи. Нарисувайте върху чист бял лист две отчетливи черни кръгчета с диаметър 3 mm. Разстоянието между центровете на кръгчетата нека бъде 5 mm. Поставете листа на добре осветено място и се отдалечете от него. Измерете разстоянието, на което преставате да различавате кръгчетата като две. Направете необходимите измервания и определете ъгъла, под който се вижда разстоянието между кръгчетата в този момент. В случай, че носите очила, можете да ги сложите по време на измерването.

• Колко пъти разделителната способност на телескопа Хъбъл е по-добра от тази на очите ви?.

Решение:

Нека ръстът на вашия приятел е  m, а търсеното разстояние до него е r . За да го виждате под ъгъл  , трябва да е изпълнено съотношението: където  α  се измерва в радиани. Първо превръщаме  в градуси и после го умножаваме по  . Така можем да пресметнем:

Впечатляващо разстояние!
Нека разстоянето, от което вече преставаме да различаваме двете черни кръгчета като две, да е m. Разстоянието между центровете на кръгчетата е m, а ъгълът, под който ги виждаме, да означим с δ . От съотношението    намираме:

където  δ  се измерва в радиани. Можем да го превърнем в градуси, а после и в минути:

Разделителната способност на нормалното човешко зрение е около 2 дъгови минути.
Сравняваме разделителната способност на телескопа Хъбъл с тази на нашите очи:

С телескопа Хъбъл можем да различаваме детайли от космическите обекти с 1000 пъти по-малки ъглови размери от тези, които можем да различим с невъоръжено око. Разделителната способност на космическия телескоп е около 1000 пъто по-добра от разделителната спосочност на нашите очи.

4 задача. Древногръцкият философ Филолай смятал, че Луната е прекрасен свят, където времето винаги е приятно и безоблачно. Според него там живеят красиви животни, 15 пъти по-едри от земните, защото лунният ден е 15 пъти по-дълъг от земния ден.
• Има ли нещо вярно в предположенията на Филолай?
• Колко време продължава лунното денонощие?

Решение:

Дали Луната е прекрасен свят, зависи от гледната точка, от която я възприемаме. За астрономите, които са я избрали като обект на изследване, сигурно е така. Времето там наистина е винаги безоблачно, понеже няма достатъчно летливи вещества, от които да се образуват облаци, нито атмосфера, в която облаците да плуват. Едва ли на някого времето ще  се стори приятно, тъй като през деня температурата на повърхността е около +130° С, а през нощта спада до –170° С. За съжаление Луната е напълно лишена от живот и красиви животни там няма.
Луната показва фази, които се сменят с период приблизително 29.5 денонощия – един синодичен лунен месец. Те зависят от различното разположение на Слънцето, Луната и Земята в различни моменти от време. Луната е обърната все с една и съща страна към нас. Да си представим наблюдател, намиращ се около центъра на видимия от Земята лунен диск. Когато Луната за нас е в пълнолуние, за този лунен наблюдател Слънцето ще е близо до зенита – това ще съответства на момента пладне в неговия лунен ден. Периодът от пълнолуние до пълнолуние е един синодичен лунен месец. Той ще се равнява на периода от пладне до пладне, или на едно слънчево денонощие за лунния наблюдател. Това означава, че лунното денонощие продължава 29.5 земни денонощия. Също толкова пъти средно трябва лунният ден да е по-дълъг от земния ден. Следователно Филолай греши, като счита, че лунният ден е само 15 пъти по-дълъг от земния.

5 задача. Млечният път, или нашата галактика, е огромна система от звезди. Тази система е с форма на диск.
• Какъв е диаметърът на нашата галактика? На какво разстояние се намира Слънцето от центъра на галактичния диск?
• Нарисувайте схема на галактичния диск, погледнат „отгоре”. Отбележете примерното положение на Слънцето, като спазите мащаба на разстоянията.
• Потърсете информация за движението на Слънцето около центъра на Галактиката. Отбележете върху вашата схема приблизително къде ще се намира Слънцето след 100 милиона години.
• На какво разстояние ще бъде тогава Слънцето от сегашното си положение в Галактиката?

Решение:

На небето виждаме Млечния път като светла ивица. Това е дискът на Галактиката, обърнат с тясната си страна към нас (ребром). Трябва да се отдалечим на доста голямо разстояние от Галактиката, за да я видим откъм плоската страна на диска.

Диаметърът на нашата галактика е около 100 000 светлинни години (или около 30 000 парсека). Представяме я схематично като кръг. Слънцето се намира на разстояние от центъра й приблизително 26 000 светлинни години (или около 8000 парсека). Следователно можем да нанесем неговото положение в точка 1, която е отдалечена от центъра на Галактиката приблизително на половината от радиуса на кръга. Слънцето се движи около центъра на Галактиката със скорост 220 km/sec и прави една обиколка приблизително за 220 000 000 години.
Интервалът от 100 000 години е почти половината от периода на обикаляне на Слънцето около галактичния център.Следователно след 100 000 години Слънцето ще се намира приблизително в диаметрално противоположната част на Галактиката, примерно в точка 2 на схемата. То е на разстояние 2 × 26 000 = 52 000 светлинни години (или около 16000 парсека) от сегашното си положение в Галактиката. (Забележка: Поради това, че определянето на размерите на нашата галактика и на положението на Слънцето в нея е трудно, получените от науката резултати са доста приблизителни. Ето защо в различни източници на информация могат да се намерят леко различаващи се данни за диаметъра на Галактиката, разстоянието от Слънцето до нейния център, скоростта и периода на движението на Слънцето. Решенията на задачата, в които са използвани такива различни данни, следва да се считат за правилни, независимо че не са получени точно същите отговори, както в предлаганото официално решение.)

6 задача.
• Потърсете звездна карта. Научете как изглежда съзвездието Касиопея (Cassiopeia). При ясно време наблюдавайте звездното небе. Опитайте се да откриете съзвездието Касиопея. Във вечерните часове през декември и януари то се вижда много високо в небето, съвсем леко на север-североизток.
• Определете приблизително ъгловите разстояния между някои от ярките звезди в съзвездието Касиопея. Използвайте ръката си и примерните мерки, дадени на рисунката. При измерванията ръката ви трябва да е опъната.
• Направете рисунка на съвездието и означете на нея измерените от вас разстояния между звездите в градуси. Запишете също датата и времето на наблюдението.

Решение:

Касиопея е сравнително малко красиво съзвездие, чиито пет най-ярки звезди образуват лесно разпознаваема фигура, наподобяваща латинската буква W. На фигурата е показано съзвездието Касиопея с приблизителните ъглови отстояния между някои от звездите.

31 декември 2008 г.
23 ч. 00 мин.