|
МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА ПО АСТРОНОМИЯ
ХІ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
І кръг
Ученици от 11-12 клас
1 задача.
През настоящата година се навършиха 50 години от изстрелването на първия изкуствен спътник на Земята. Спътникът е бил в орбита около нашата планета от 4 октомври 1957 г. до 4 януари 1958 г. Орбитата му е била с наклон 65.1° към равнината на земния екватор. Перигеят на орбитата му е бил над северното полукълбо на височина 228 km над земната повърхност, а апогеят е бил на височина 947 km. Спътникът е преминавал по небето като малка светеща точка и земните жители са могли да видят първото сътворено от тях самите космическо тяло.
Имало ли е области по земното кълбо, където спътникът не се е появявал над хоризонта? Ако е имало, какви са техните граници? Ако не е имало, обяснете своя отговор и го подкрепете с пресмятания.
Решение:
Нека перигеят на спътника е точката ХР, а апогеят – точката ХА . Наклонът на орбитата му към екватора на Земята е  . Очевидно за точките от земната повърхност, разположени между 65.1° северна и южна ширина спътникът ще се появява над хоризонта. . Очевидно за точките от земната повърхност, разположени между 65.1° северна и южна ширина спътникът ще се появява над хоризонта.

Да разгледаме най-неблагоприятния случай – перигеят на спътника е в най-северната точка от неговата орбита. Когато спътникът е в перигей, зоната, в която той ще се вижда над хоризонта, ще достига в северна посока до точка А. Тази точка се намира по земната повърхност на ъгъл a от точката, за която в същия момент спътникът е в зенита. Пресмятаме ъгъла:

където  km е радиусът на Земята. Получаваме km е радиусът на Земята. Получаваме 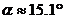 . Следователно точката А се намира на географска ширина . Следователно точката А се намира на географска ширина  . Това означава, че спътникът не се е появявал над хоризонта за областта около Северния полюс с радиус приблизително . Това означава, че спътникът не се е появявал над хоризонта за областта около Северния полюс с радиус приблизително  . Ако отчетем и рефракцията, то областта, в която спътникът не се е появявал над хоризонта, ще стане още по-малка. . Ако отчетем и рефракцията, то областта, в която спътникът не се е появявал над хоризонта, ще стане още по-малка.
Ако перигеят на спътника не е бил в най-северната точка от орбитата му, то зоната около северния полюс, в която той не се е появявал над хоризонта, се стеснява още повече.
Аналогично за точката В в южното полукълбо можем да пресметнем ъгъла b . Тя отстои на такъв ъгъл от точката, за която спътникът е в апогей.


Тъй като  , то тази точка е “отвъд” Южния полюс. Това означава, че в южното полукълбо няма точки, за които спътникът да не се е появявал над хоризонта. , то тази точка е “отвъд” Южния полюс. Това означава, че в южното полукълбо няма точки, за които спътникът да не се е появявал над хоризонта.
2 задача.
• Кой край на слънчевия диск започва да се закрива в началото на слънчевото затъмнение – източният или западният?
• Кой край на лунния диск започва да се закрива в началото на лунното затъмнение – източният или западният? Обяснете своите отговори.
Решение:
Луната обикаля около Земята от запад на изток. Ето защо, когато настъпва слънчево затъмнение, Луната започва първо да закрива западния край на видимия слънчев диск.
При лунно затъмнение Луната навлиза в земната сянка откъм западния край на тази сянка. Затова тогава първи започва да потъмнява източният край на лунния диск.

3 задача. Разделителната способност на космическия телескоп Хъбъл (Hubble Space Telescope) е около 0.1″ (дъгови секунди). Това е най-малкото видимо ъглово отстояние мeжду две звезди, при което те биха могли да се различат като отделни звезди с телескопа.
• На какво разстояние от вас трябва да застане ваш приятел, за да го виждате под такъв ъгъл? При пресмятанията посочете ръста на вашия приятел.
• Определете разделителната способност на вашите очи. Нарисувайте върху чист бял лист две отчетливи черни кръгчета с диаметър 3 mm. Разстоянието между центровете на кръгчетата нека бъде 5 mm. Поставете листа на добре осветено място и се отдалечете от него. Измерете разстоянието, на което преставате да различавате кръгчетата като две. Направете необходимите измервания и определете ъгъла, под който се вижда разстоянието между кръгчетата в този момент. В случай, че носите очила, можете да ги сложите по време на измерването.

• Колко пъти разделителната способност на телескопа Хъбъл е по-добра от тази на очите ви?.
Решение:
Нека ръстът на вашия приятел е  m, а търсеното разстояние до него е r . За да го виждате под ъгъл m, а търсеното разстояние до него е r . За да го виждате под ъгъл  , трябва да е изпълнено съотношението: , трябва да е изпълнено съотношението:  където α се измерва в радиани. Първо превръщаме където α се измерва в радиани. Първо превръщаме  в градуси и после го умножаваме по в градуси и после го умножаваме по  . Така можем да пресметнем: . Така можем да пресметнем:


Впечатляващо разстояние!
Нека разстоянето, от което вече преставаме да различаваме двете черни кръгчета като две, да е  m. Разстоянието между центровете на кръгчетата е m. Разстоянието между центровете на кръгчетата е  m, а ъгълът, под който ги виждаме, да означим с δ . От съотношението m, а ъгълът, под който ги виждаме, да означим с δ . От съотношението  намираме: намираме:

където δ се измерва в радиани. Можем да го превърнем в градуси, а после и в минути:


Разделителната способност на нормалното човешко зрение е около 2 дъгови минути.
Сравняваме разделителната способност на телескопа Хъбъл с тази на нашите очи:

С телескопа Хъбъл можем да различаваме детайли от космическите обекти с 1000 пъти по-малки ъглови размери от тези, които можем да различим с невъоръжено око. Разделителната способност на космическия телескоп е около 1000 пъто по-добра от разделителната спосочност на нашите очи.
4 задача. Древногръцкият философ Филолай смятал, че Луната е прекрасен свят, където времето винаги е приятно и безоблачно. Според него там живеят красиви животни, 15 пъти по-едри от земните, защото лунният ден е 15 пъти по-дълъг от земния ден.
• Има ли нещо вярно в предположенията на Филолай?
• Колко време продължава лунното денонощие?
• От какви фактори зависи продължителността на лунното денонощие? Обяснете качествено как се изменя тази продължителност в зависимост от всеки от факторите.
Решение:
Дали Луната е прекрасен свят, зависи от гледната точка, от която я възприемаме. За астрономите, които са я избрали като обект на изследване, сигурно е така. Времето там наистина е винаги безоблачно, понеже няма достатъчно летливи вещества, от които да се образуват облаци, нито атмосфера, в която облаците да плуват. Едва ли на някого времето ще се стори приятно, тъй като през деня температурата на повърхността е около +130° С, а през нощта спада до –170° С. За съжаление Луната е напълно лишена от живот и красиви животни там няма.
Луната показва фази, които се сменят с период приблизително 29.5 денонощия – един синодичен лунен месец. Те зависят от различното разположение на Слънцето, Луната и Земята в различни моменти от време. Луната е обърната все с една и съща страна към нас. Да си представим наблюдател, намиращ се около центъра на видимия от Земята лунен диск. Когато Луната за нас е в пълнолуние, за този лунен наблюдател Слънцето ще е близо до зенита – това ще съответства на момента пладне в неговия лунен ден. Периодът от пълнолуние до пълнолуние е един синодичен лунен месец. Той ще се равнява на периода от пладне до пладне, или на едно слънчево денонощие за лунния наблюдател. Това означава, че лунното денонощие продължава 29.5 земни денонощия. Също толкова пъти средно трябва лунният ден да е по-дълъг от земния ден. Следователно Филолай греши, като счита, че лунният ден е само 15 пъти по-дълъг от земния.
Под продължителност на лунното денонощие тук разбираме слънчевото денонощие за Луната – интервалът от време между две, примерно горни кулминации на Слънцето. Продължителността му зависи от ъгловата скорост, с която става видимото денонощно движение на Слънцето по лунното небе от изток на запад. Това движение се определя от околоосното въртене на Луната. Върху него обаче се наслагва макар и по-бавното преместване на Слънцето на фона на звездите в обратна посока – от запад на изток. Това преместване води до намаляване на ъгловата скорост на денонощното движение на Слънцто и до увеличение на продължителността на слънчевото денонощие за лунния наблюдател. Видимото преместване на Слънцето на фона на звездите се дължи на движението на Луната относно Слънцето. Върху него влияят следните фактори:
- Елиптичност на земната орбита около Слънцето. Когато Земята е около перихелия на своята орбита, тя се движи по-бързо, а заедно с нея и Луната, която е гравитационно свързана със Земята. Когато Земята е в афелия на своята орбита, тя заедно с Луната се движи по-бавно. Това означава, че около перихелия на земната орбита лунното денонощие ще е по-дълго, а около афелия – по-кратко.
- Наклон на лунния екватор към равнината на еклиптиката. Да въведем лунни небесни координати, подобно на екваториалните небесни координати за земния наблюдател – ректасцензия и деклинация. Наклонът на лунния небесен екватор към еклиптиката е много малък – около 2 градуса. Но все пак той влияе върху видимата скорост на преместване на проекцията на Слънцето върху лунния небесен екватор. Около лунните “равноденствия”, когато Слънцето е близо до лунните равноденствени точки, проекцията му върху лунния небесен екватор се премества най-бавно. Това скъсява слънчевите денонощия за лунния наблюдател. Когато Слънцето е близо до точките на слънцестоене в лунната координатна система, проекцията му върху лунния небесен екватор се премества по-бързо и денонощията се удължават.
- Елиптичност на лунната орбита около Земята. Аномалистичният лунен месец – периодът между две преминавания на Луната през перигея на нейната орбита – е по-кратък от синодичния. В зависимост от различната ориентация на лунната орбита относно Слънцето, в рамките на един синодичен месец могат да се случат две преминавания на Луната през перигея и едно през апогея, или пък две преминавания на Луната през апогея и едно през перигея. Като имаме предвид втория закон на Кеплер, заключаваме, че в тези два случая продължителността на синодичния лунен месец, а оттам и на лунното денонощие, ще е различна.
(Забележка: Последните две обяснения, дадени в курсив, са по-сложни и не може да се изискват от участниците в първия кръг като задължителен елемент от решението. Ако определен участник е дал в решението си някои от идеите в тях, то да му се присъждат допълнителните точки за награда).
5 задача. Древногръцкият астроном Анаксагор, живял в V в.пр.н.е., е бил убеден, че Земята е плоска. Още тогава се знаело, обаче, че за даден момент от едно денонощие височината на Слънцето над хоризонта зависи от положението на наблюдателя по меридиана. Анаксагор обяснява това с паралактично отместване на Слънцето. Дори са били правени опити, като се използва обяснението на Анаксагор, да се определи разстоянието до Слънцето.
• Какво минимално разстояние до Слънцето би се получило при такъв опит? (Упътване: Изберете момента на наблюдението да е пладне и точки на наблюдение, за които Слънцето е близо до зенита.)
• С какви наблюдения бихте опровергали теорията на Анаксагор?
Решение:
Да си представим две точки А и В, лежащи върху един и същ земен меридиан на ъглово разстояние Δφ0 по географска ширина (Фиг. 1). Линейното разстояние между двете точки ще бъде:
 (1) (1)
където  km е радиусът на Земята, а Δφ0 се измерва в радиани. km е радиусът на Земята, а Δφ0 се измерва в радиани.

Фиг. 1
Нека за наблюдател в точка А Слънцето да е в зенита. Тогава в същия момент за наблюдател в точка В то ще отстои на ъгъл δ0’ от зенита. Отбелязваме с δ0 ъгъла, който е равен на видимото паралактично отместване на Слънцето при преместването от точка А в точка В. Ъгълът δ0’ е външен за триъгълника, образуван от точките О, В и Слънцето. Следователно:

Като имаме предвид, че  , ако измерванията ни не са с голяма точност, можем да приемем: , ако измерванията ни не са с голяма точност, можем да приемем:  . Т.е. видимото ъглово отместване на Слънцето при преместване от точка А в точка В е приблизително равно на разликата между географските ширини на двете точки. . Т.е. видимото ъглово отместване на Слънцето при преместване от точка А в точка В е приблизително равно на разликата между географските ширини на двете точки.
Нека сега да смятаме, подобно на Анаксагор, че Земята е плоска (Фиг. 2). За точка Нека за точка А Слънцето е в зенита. За наблюдател в точка В в същия момент Слънцето ще е отклонено на ъгъл δ’ от зенита. От чертежа е ясно, че  . Съгласно теорията на Анаксагор, трябва да считаме, че d е видимото паралактично отместване на Слънцето при преместване от точка А в точка В. Така за разстоянието до Слънцето можем да напишем: . Съгласно теорията на Анаксагор, трябва да считаме, че d е видимото паралактично отместване на Слънцето при преместване от точка А в точка В. Така за разстоянието до Слънцето можем да напишем:

Ако вземем точка В да бъде на много малко разстояние от А, в сравнение с разстоянието до Слънцето, то можем да използваме приближението:

Но сега нека си спомним, че в действителност ъгловото отстояние  на Слънцето от зенита в точка В е същото като ъгъла δ0’ на Фиг. 1, а той е приблизително равен на Δφ0. на Слънцето от зенита в точка В е същото като ъгъла δ0’ на Фиг. 1, а той е приблизително равен на Δφ0.

Фиг. 2
Следователно:

Но като сравним с равенството (1), ще получим, че разстоянието от “плоската Земя” до Слънцето е:  , или колкото е радиусът на истинската Земя. За да опровергаем теорията на Анаксагор, взимаме трета точка, която е на значително по-голямо разстояние s от точка А (Фиг. 3). , или колкото е радиусът на истинската Земя. За да опровергаем теорията на Анаксагор, взимаме трета точка, която е на значително по-голямо разстояние s от точка А (Фиг. 3).

Фиг. 3
Нека първо считаме, че Земята е плоска. Отбелязваме нашата точка с C (разстоянието AC = s). За точка А Слънцето е в зенита. При преместване на наблюдателя в точка C’, би трябвало да се наблюдава видимо отстояние на Слънцето от зенита на ъгъл δ1. Това е видимото паралактично отместване на Слънцето, съгласно Анаксагор. Очевидно трябва да е изпълнено съотношението:

Можем да проверим това, като използваме стойността на разстоянието до Слънцето  km, която изчислихме по-горе. В действителност обаче, ако наистина извършим съответните наблюдения и измервания, ще получим друго. Поради кръглата форма на Земята, отдалечавайки се на разстояние s от точка А, ние ще се озовем не в точка C, а в точка С’ (Фиг. 3). При това разстоянието s ще бъде дължината на дъгата АС’ по земната повърхност. Измереното от нас ъглово отместване на Слънцето ще бъде не δ1, а km, която изчислихме по-горе. В действителност обаче, ако наистина извършим съответните наблюдения и измервания, ще получим друго. Поради кръглата форма на Земята, отдалечавайки се на разстояние s от точка А, ние ще се озовем не в точка C, а в точка С’ (Фиг. 3). При това разстоянието s ще бъде дължината на дъгата АС’ по земната повърхност. Измереното от нас ъглово отместване на Слънцето ще бъде не δ1, а  . То няма да се подчинява на горното съотношение. Колкото по-далеч се намира точката С’ от А, толкова разликата ще бъде по-значителна. Така ние ще докажем, че Земята не е плоска и Анаксатор не е прав. . То няма да се подчинява на горното съотношение. Колкото по-далеч се намира точката С’ от А, толкова разликата ще бъде по-значителна. Така ние ще докажем, че Земята не е плоска и Анаксатор не е прав.
Същото може да се докаже и ако се разгледа някакъв пример с конкретни стойности на разстоянието s и ъгъла  . .
Нека например точка С да е отдалечена от А на разстояние  по плоската Земя, т.е. на същото разстояние, каквото е разстоянието от Земята до Слънцето, получено съгласно предположението на Анаксагор. по плоската Земя, т.е. на същото разстояние, каквото е разстоянието от Земята до Слънцето, получено съгласно предположението на Анаксагор.

Фиг. 4
От Фиг. 4 виждаме, че в такъв случай за точка С Слънцето ще трябва да се наблюдава на 45° от зенита. Ако направим измерването по истинската кръгла Земя, обаче, на разстояние  ще се озовем в точка С’. Тя ще отстои по географска ширина от точка А на ъгъл, равен на един радиан, или ще се озовем в точка С’. Тя ще отстои по географска ширина от точка А на ъгъл, равен на един радиан, или  . Приблизително такова ще бъде и реално измереното от нас зенитно отстояние на Слънцето за точка С’. Така че стойността, която ще получим, ще се различава значително от предположението, произтичащо от теорията на Анаксагор. . Приблизително такова ще бъде и реално измереното от нас зенитно отстояние на Слънцето за точка С’. Така че стойността, която ще получим, ще се различава значително от предположението, произтичащо от теорията на Анаксагор.
6 задача. Двама пилоти се състезават със своите самолети. Те излитат от Санкт Петербург (φ ≈ 60° с.ш., λ ≈ 30° и.д.) в Русия. Целта им е да стигнат най-бързо до Анкоридж (Anchorage, φ ≈ 60° с.ш., λ ≈ 150° з.д.) в Аляска. Самолетите им се движат със скорост 1000 km/h. Единият пилот избира източния път – движи се през цялото време само на изток. Другият избира западния път.
• Пресметнете времената, за които пилотите са стигнали до Анкоридж.
• Ако вие трябваше да се състезавате, кой път бихте избрали? Подкрепете отговора си с пресмятания.
Решение:
Забелязваме, че двата града имат еднаква географска ширина – лежат на един и същ паралел. Географските им дължини се различават със 180°, т.е. те са в две диаметрално противоположни точки от този паралел. Пилотът, който се движи само на изток, ще лети през цялото време по едната половина на паралела, а пилотът, избрал западния път – по другата. Пътищата на двамата пилоти са еднакви по дължина. Тъй като се движат с еднаква скорост, те са пристигнали едновременно в Анкоридж – победител в състезанието няма.

Всеки от пилотите е изминал половината от 60-градусовия паралел. Да разгледаме защрихования правоъгълен триъгълник на чертежа. В него радиусът на паралела r лежи срещу ъгъл от 30° и следователно е двойно по-малък от земния радиус  km. Дължината на пътя на всеки от пилотите е: km. Дължината на пътя на всеки от пилотите е:
 km km
Със скорост 1000 km/h този път пилотите ще изминат за 10 часа.
Ако вие искате да победите пилотите в състезанието, трябва да изберете северния път – пътят, минаващ през северния полюс на Земята. Той представлява дъга от голям кръг по земната повърхност, съответстваща на ъгъл  . Нейната дължина е 1/6 от обиколката на Земятя, или: . Нейната дължина е 1/6 от обиколката на Земятя, или:
 km km
Този път вие бихте изминали приблизително за 6 часа и 40 мин. И бихте спечелили състезанието със значителна преднина.
|
|