МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА

ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА ПО АСТРОНОМИЯ

ХIV НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ

http://astro-olymp.org

  Ученици младша възраст (до 16 г.)

1 задача. Юпитер. Вие сте изследователи на Юпитер и наблюдавате с нов и много съвършен телескоп любимата си планета. На снимката е показана прекрасната гледка, която се разкрива пред вашия поглед. Спътникът Йо хвърля своята сянка върху облачната атмосфера на Юпитер.

• Необходимо ли ще бъде  да бодърствате до ранните утринни часове, за да изгрее Юпитер и да видите тази гледка? Обосновете своя отговор.

• Как ще се променят условията на видимост на планетата от тази нощ нататък – ще се удължава ли или ще се скъсява времето от нощта, през което Юпитер ще може да се наблюдава? Защо?

• Как ще се променя разстоянието между Юпитер и Земята – ще се увеличава или ще намалява? Дайте обяснение.

Решение:
Както знаем, Голямото червено петно – най-големият атмодферен вихър в Слънчевата система – се намира в южното полукълбо на Юпитер. Следователно на снимката северният полюс на планетата е нагоре, а сянката на Йо е отместена на изток от спътника. Петното заедно със сянката се намират в западната част на видимия диск на Юпитер. Отместването на сянката спрямо видимото положение на спътника е сравнително малко. В мястото на сянката слънчевите лъчи падат към повърхността на Юпитер под ъгъл близък до 90°. Всичко това означава, че Слънцето се намира по небесната сфера западно от Юпитер и то на много голямо ъглово отстояние – то е почти „зад нас”. Оттук заключаваме, че Юпитер изгрява от източната част на хоризонта не много дълго преди залеза на Слънцето и се вижда през почти цялата останала нощ. Ето защо няма да ни се наложи да чакаме изгрева на планетата до утринните часове, а напротив, ще можем да я наблюдаваме през по-голямата част от нощта.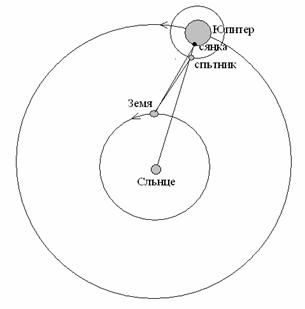

С течение на времето поради орбиталното си движение Юпитер би трябвало да се премества от запад на изток. Земята, обаче, се движи по своята орбита значително по-бързо от Юпитер и го „изпреварва”. Конфигурацията на снимката показва, че благодарение на това моментът на противостоене на Юпитер вече е отминал. Около този момент условията за видимост на планетата са били най-добри, защото тя е изгрявала със залеза на Слънцето и се е виждала през цялата нощ. Освен това тогава разстоянието между Земята и Юпитер е било най-малко.
Оттам нататък Юпитер изгрява все по-рано и периодът му на виидимост се скъсява. Това ще продължи още и доста време след момента, в който е направена снимката. Разстоянието от Земята до Юпитер постепенно ще се увеличава.

Критерии за оценяване (12 т.):
За правилно съобразяване на ориентацията на Юпитер по Голямото червено петно – 1 т.
За правилни разсъждения свързващи взаимните разположения на спътника, сянката и видимия диск на планетата от една страна, и положението на Слънцето и Юпитер относно Земята – 5 т.
За правилни разсъждения и заключения относно условията на видимост на Юпитер в момента на снимката – 2 т.
За правилни разсъждения и отговор на въпроса как ще се изменят условията на видимост след този момент – 3 т.
За правилни заключения относно изменението на разстоянието до Юпитер – 2 т.

2 задача. Завръщане на Земята. Смелият космонавт Байрям Байрямали се завръща на родната Земя след далечно пътешествие със субсветлинна скорост. Поради ефектите от теорията на относителността, за него полетът е продължил няколко години, но на Земята са минали много повече. Всичко се е променило. Останала е същата само хижа Бузлуджа (φ ≈ 42°), където Байрям отива, воден от носталгични спомени. Около полунощ той с удивление вижда близо до зенита Полярната звезда.

• Приблизително колко години трябва да са минали на Земята, докато Бяйрям е летял в космоса? Оценете минималния възможен период.

• В кой сезон от годината е отишъл Байрям на хижа Бузлуджа?

Обяснете вашите отговори.

Решение:
Височината на северния небесен полюс над хоризонта е равна на географската ширина на наблюдателното място. В случая за хижа Бузлуджа  височината е 42°. Зенитното отстояние на северния небесен полюс ще бъде   90° – φ = 48°. Това зенитно отстояние е много близко до удвоената стойност на наклона на земната ос към оста на еклиптиката   2ε = 2×23.5° = 47°. Както знаем, поради прецесията на земната ос северният небесен полюс извършва кръгово движение около полюса на еклиптиката и периодът на това движение е около 26 000 години. Но движението на северния небесен полюс се извършва на фона на звездите – той се мести спрямо тях. За земния наблюдател, обаче, северният небесен полюс си остава винаги със същите височина и азимут. За времето на полета на Байрям северният небесен полюс е изменил видимото си положение спрямо Полярната звезда с ъгъл близък до 2ε. Това означава, че северният небесен полюс е пропътувал по небесната сфера половината от един цикъл на прецесия – преместил се е в противоположната точка на окръжността, която описва около еклиптичния полюс. Следователно, докато Байрям е летял в космоса, на Земята са изминали около 13 000 години. Това е минималният възможен период. Разбира се, може да са изминали и по-дълги периоди, които се получават като към 13 000 години прибавим цяло число периоди на прецесия – цяло число пъти по 26 000 години.

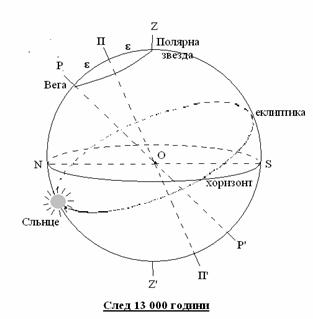
Участниците в школата може би знаят, че Полярната звезда и звездата Вега са разположени почти симетрично от двете страни на северния полюс на еклиптиката, който е в Дракон. Следователно след 13 000 години северният небесен полюс ще е недалеч именно от звездата Вега. Те  вероятно са забелязали, че около полунощ към края на наблюдателните занятия звездата Вега е близо до горна кулминация. Щом при завръщането си на хижа Бузлуджа Байрям вижда Полярната звезда ще е в горна кулминация в полунащ. Следователно Слънцето, което ще е в долна кулминация тогава, ще бъде в противоположно положение по еклиптиката, спрямо положението си сега, по време на школата. Но и ориентацията на земната ос спрямо Слънцето тогава ще бъде противоположна на сегашната. Значи тогава годишният сезон е същият като сезона, в който се провежда школата – юли месец. Ето защо Байрям трябва да е там през лятото.

Критерии за оценяване:
За обяснение на появата на Полярната звезда в зенита с прецесията – 2 т.
За правилни разсъждения относно определяне на периода от време, изтекъл на Земята – 4 т.
За правилен числен отговор – 1 т.
За правилни разсъждения относно годишния сезон – 4 т.
За правилен отговор кой ще бъде сезонът – 1 т.      

3 задача. Небето се усмихва.  На 1 декември 2008 г. небето весело ни се е усмихнало чрез Луната и планетите Венера и Юпитер. Снимката е направена в австралийския град Сидней (φ = 34.5° ю.ш.).  

• Приблизително в каква фаза е била тогава Луната?

• В коя част от нощта е направена снимката?

• Приблизително в каква посока се вижда Луната?

• Нарисувайте схема с приблизителните положения на Венера и Юпитер по техните орбити спрямо Земята и Слънцето.

• Как биха могли да изглеждат Юпитер и Венера, ако ги погледнем в телескоп в този момент?

• Оценете приблизително звездната величина на Юпитер в момента, когато е направена снимката, като знаете, че звездната му величина при максимален блясък е –2.7^m.

Венера е на 0.7 астрономически единици от Слънцето, а Юпитер на 5.2 астрономически единици.

Решение:
Луната на снимката изглежда като тънък сърп. Това означава, че тя е на възраст малко преди или малко след новолуние. Означава също така, че Слънцето се намира на неглямо видимо ъглово разстояние от Луната. Лунният сърп е обърнат с изпъкналата си страна наляво и надолу. В тази посока трябва да е и Слънцето. Тъй като Сидней е в южното полукълбо на Земята, заключаваме, че фазата на Луната е малко след новолуние, а Слънцето преди не много време е залязло под хоризонта. Следователно снимката е направена вечерта. Точката на залеза на Слънцето трябва да е в посоко изток-югоизток, понеже датата е 1 декември – скоро предстои лятното слънцестояние за южното полукълбо, когато Слънцето има най-голяма отрицателна деклинация.   Близка до тази е и посоката, в която виждаме Луната.

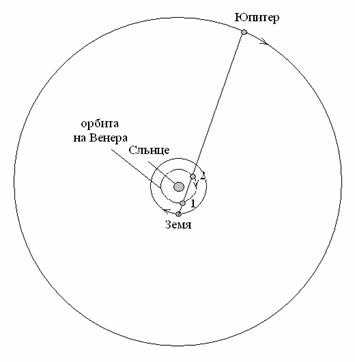
Понеже сме в южното полукълбо, нека построим схемата на положенията на планените, гледана откъм южния полюс на Земята. Затова движението на планетите около Слънцето ще бъде по часовниковата стрелка. Като знаем, че видимият ъглов размер на Луната е около 0.5° и го съпоставим с отстоянието на двете планети от нея, виждаме, че то е твърде малко, а също можем да кажем, че двете планети заедно с Луната са на сравнително малко ъглово отстояние и от Слънцето. Ето защо можем да заключим, че Юпитер е в положение малко след горно съединение.
Венера по принцип би могла да бъде в положение 1 или 2 по своята орбита. Имайки предвид блясъка й, считаме, че е по-вероятно да е в положение 2, понеже в положение 1 тя би изглеждала като много тънък сърп, подобно на Луната, и не би била така ярка. Ако наблюдаваме планетите с телескоп, както Венера, така и Юпитер биха изглеждали като светли кръгове, защото са обърнати към Земята почти изцяло с осветените си от Слънцето страни.
За определяне на звездната величина на Юпитер можем да считаме, че той е приблизително в горно съединение. Максимален блясък Юпитер би имал очевидно в противостояние. Разстоянията Земя-Юпитер при противостояние и горно съединение се отнасят както:

(5.2 а.е. – 1 а.е.) / (5.2 а.е. + 1 а.е.) ≈ 0.677

В сила е съотношението: 

Е₁ / Е₂ = 1 / 0.6772  ≈ 2.182

където  Е₁  и  Е₂  са осветеностите, създавани на Земята от Юпитер съответно в противостояние и в съединение. Тогава чрез формулата на Погсън намираме:

lg (Е₁ / Е₂) = 0.4(m₂ – m₁)

където    m₁  и   m₂  са звездните величини на Юпитер в противостояние и в съединение. Накрая получаваме:  

m₂ = m₁ + 2.5 lg (Е₁ / Е₂) ≈ –1.85^m .

Критерии за оценяване (12 т.):
За правилно определяне на фазата на Луната  - 2 т.
За определяне на времето от нощта, когато е направена снимката – 2 т.
За определяне на посоката – 2 т.
За построяване на схемата – 2 т.
За обяснение как биха изглеждали планетите в телескоп –   1 т.
За пресмятане на звездната величина на Юпитер – 3 т.

Задача 4. Непозната планета. Поради проблем в корабната система за управление (причинен от изкъртен радиатор), звездните навигатори Маги и Петко кацат аварийно на непозната планета.  Скоро повредата е отстранена, но Маги и Петко не знаят дали горивото ще им стигне, за да стартират от планетата. Веднага започват наблюдения и изследвания. Разбират, че на повърхността на планетата тежат два пъти по-малко, отколкото на Земята. Определят орбиталния период на единствения спътник на планетата, който се оказва 40 земни денонощия. Установяват, че видимият ъглов диаметър на спътника е 5′.05, когато се вижда в зенита, и 5′, когато е на хоризонта.

• Как по тези наблюдателни данни може да се определят масата и радиусът на непознатата планета?

• Пресметнете втора космическа скорост за тази планета  (γ = 6.67× 10^-11м³/кг.с²).

Решение:
Да означим радиуса на непознатата планета с R , а масата й с М. Ускорението на силата на тежестта на нейната повърхност ще бъде:

g* = γM / R²                                 (1)

където  γ  е грвитационната константа. Звездните навигатори са открили, на непознатата планета тежат два пъти по-малко, отколкото на Земята, следователно:

g* = g / 2                                   (2)

където   g = 9.8 m/s²   е земното ускорение.
За орбиталното движение на спътника, съгласно ІІІ закон на Кеплер можем да напишем:

r³/ T² = γM / 4π²                            (3)

където  r  е радиусът на орбитата на спътника, а Т е орбиталният му период.

Както се вижда от схемата, когато наблюдаваме спътника на хоризонта, ние го виждаме от разстояние, приблизително равно на радиуса на орбитата му r . Когато го наблюдаваме в зенита, разстоянието от нас до него е намалено с радиуса на планетата R. За видимите ъглови размери Δ_z  и Δ_h на спътника в зенита и на хоризонта можем да напишем:

Δ_z  / Δ_h = 5′.05 / 5′
Δ_z  / Δ_h = r / (r – R)

От последното съотношение намираме:

r / R = 100                                  (4)

От уравненията (1) и (2) получаваме:

g / 2 = γM / R²                              (5)

Разделяме почленно уравненията (3) и (5) и получаване:

r³ / R² = gT² / 8π²

Имайки предвед (4), за разстоянието до спътника и радиуса на планетата получаваме:

r ≈ 148 000 km ,                   R ≈ 1480 km

От (5) за масата на планетата получаваме:

M = gR² / 2γ ≈ 1.6 × 10²³ kg

За втора космическа скорост намираме:

v = (2γM / R)^1/2 ≈ 3.8 km/s

Критерии за оценяване (12 т.):
За определяне на ускорението насилата на тежестта на планетата – 1 т.
За правилни идеи за определяне на радиуса и масата на планетата – 2 т.
За правилно съставяне на уравненията – 3 т.
За вярни алгебрични пресмятания на r, R, M - 2 т.
За верни числени отговори за R, M  - 2 т.
За определяне на втора космическа скорост – 2 т.

Задача 5. Повреден телескоп. След дълга употреба по време на школи за подготовка на млади астрономи механизмите на един телескоп се повредили. Телескопът бил с азимутална монтировка и можел да се насочва в различни посоки само по азимут. Височината му над хоризонта не можела да се променя. Младите астрономи, работещи с него, установили, че могат да наблюдават цялото северно небе, но не и южното.

• На каква височина над хоризонта е блокиран телескопът?

• На каква географска ширина се намира обсерваторията, където е той?

Рефракцията и размерите на зрителното поле на телескопа да не се отчитат.

Решение:
Според условието на задачата, с телескопа може да се наблюдава само цялата северна небесна полусфера и никаква част от южната. Следователно, когато телескопът е насочен точно на юг, то той всъщност трябва да сочи точно към небесния екватор.
От тук следва, че ако означим географската ширина на мястото на наблюдение с φ, то височината, на която телескопът е блокиран, е h = 90° - φ.
Понеже се намираме в северното полукълбо на Земята, то въртейки го по азимут, от точката юг. ние всъщност увеличаваме деклинацията към която той е насочен.
Отново обръщаме внимание на факта, че с телескопа можем да наблюдаваме цялата северна небесна полусфера. Това означава, че въртейки го по азимут, с него ние можем да достигнем и северния небесен полюс. Той, както знаем, е разположен точно на север на височина над хоризонта, равна на географската ширина на мястото φ.
И така стигаме до извода, че височината на която телескопът е насочен, трябва да бъде равна едновременно на географската ширина на мястото на наблюдение, а също така и на 90° минус тази ширина.
От тук получаваме:

90° - φ =  φ
2φ = 90°
φ = 45°.

Очевидно и височината на която телескопът е блокирал също е 45°.

Критерии за оценяване:
За правилно съобразяване за това, че телескопът насочен на юг сочи небесният екватор – 2т.
За правилен извод за връзката между височината на телескопа и географската му ширина – 2т.
За правилен извод как се изменя деклинацията, към която телескопът е насочен, когато го въртим по азимут – 1т.
За извод, че височината на телескопа също е равна и на географската му ширина – 2т.
За правилна математическа постановка – 2т.
За правилни числени отговори – 1т.

Ученици старша възраст (до 18 г.)

1 задача. Необикновен обект. С изключително прецизни методи на изследване астрофизикът Калин Кръстев установил, че новооткритата от него неутронна звезда има диаметър 26 км. Тя се наблюдава като пулсар, чиито импулси се регистрират на Земята с честота 126 в секунда. Оценете приблизително каква е минималната възможна плътност на този обект.

Решение:
За да бъде пулсарът устойчив, то гравитацията му на повърхността трябва да надвишава центробежните сили, които възникват, вследствие на околоосното му въртене.
Нека да означим периода му на въртене около оста с T. Той е равен на интервала от време между два последователни импулса, които се регистрират от него или 1/126s ≈ 0.008s.
Означаваме ъгловата му скорост на въртене с ω = 2π/Т.
Ако радиусът на пулсара е R, то максималното центробежно ускорение, което изпитва частичка от него, намираща се на повърхността му, е а_с =ω²R. Гравитационното ускорение, което й се придава, е
g = γM/R², където M е масата на пулсара, а γ e гравитационната константа.
Нека ρ е търсената плътност. Тогава М = (4/3)πρR³. Така получаваме, че g = 4πγρR/3.
Както вече казахме, за да бъде пулсарът устойчив, трябва гравитационните сили да надвишават центробежните. От тук следва, че а_с < g , или ω²R <4πγρR/3. Като използваме, че ω = 2π/Т, получаваме:

ρ > 3π/γT²
ρ > 2,24×10¹⁵ kg/m³.

Имайки предвид, че това е само минимална оценка, то можем да кажем, че плътността е наистина впечатляващо висока! Ето защо, тези обекти са толкова интересни за астрономите.

Критерии за оценяване
За правилни съображения кога пулсарът ще е стабилен – 3т.
За правилно изразяване на центробежните сили – 2т.
За правилно изразяване на гравитационните сили – 2т.
За правилен математически израз за плътността и правилна числена стойност – 2т.
За извод, че това е минимална оценка – 1т .

2 задача. Космически проект. Както е известно, поради елиптичната форма на марсианската орбита, Марс в противостояние може да е на значително различаващи се разстояния до Земята. Веднъж на около 17 години се случва т.нар. велико противостояние, когато има максимално сближаване на Земята и Марс.
През 2030 г. космическите инженери  Ивайло и Михаела работят по проект с фантастични мащаби за преустройство на Слънчевата система. В резултат Марс е заставен да се движи по съвсем нова кръгова орбита около Слънцето. При това той се сближава максимално със Земята веднъж на 17 години.

• Какъв би трябвало да е орбиталният период на Марс тогава? Считайте, че Земята също се движи около Слънцето по кръгова орбита.

• На какво разстояние ще се намира Марс от Земята при максимално сближаване?

• Каква ще е видимата звездна величина на Марс при максимално сближаване със Земята? Понастоящем видимата звездна величина на Марс при средно противостояние е –1,65^m. Средното разстояние на Марс от Слънцето е 1.524 астрономически единици.

Решение:
Понеже Марс е веднъж на всеки 17 години най – близо до Земята, то това е неговият синодичен период T_SYN относно нашата планета. Имайки само тази информация обаче, ние всъщност имаме две възможности: Марс да е бил оставен като външна планета, или да е бил заставен да стане вътрешна.
Ако предположим, че Марс остава външна планета дори след намесата на двамата инженери, то можем да запишем следното равенство за синодичния му период:

1/Т_SYN = 1/T_З – 1/Т_M ,

където  Т_M  е търсеният орбитален период на Марс, а       T_З = 1 година. Следователно:

Т_M = Т_SYN . T_З / (Т_SYN - T_З)
Т_M ≈ 388 денонощия

В другия случай в който Марс е бил накаран да стане вътрешна планета, за синодичния му период е в сила:

1/Т_SYN = –1/T_З + 1/Т_M ,
Т_M = Т_SYN . T_З / (Т_SYN + T_З)
Т_M ≈ 345 денонощия.

За да намерим минималното разстояние между Марс и Земята, трябва първо да изчислим радиуса на новата марсианска орбита rM. Използваме  връзката:

r [AU]³ = T [години]²

Оттук за двата случая пресмятаме:

r_M = 1,041 AU   и   r_M = 0,962 AU

Следователно, ако Марс е външна планета минималното разстояние между него и Земята е 0,041 AU, а ако е вътрешна.
Относно максималния блясък на Марс, първо ще разгледаме случая в който той е външна планета. Факторите, влияещи върху блясъка му, които се променят са следните:

• намалява разстоянието Марс – Слънце r_M , което води до по – голяма осветеност върху Марс и от там до повече отразявана светлина от него. Това увеличава яркостта на Марс за земния наблюдател;

• намалява минималното разстояние Земя – Марс r_З-М , което отново води до повишаване на видимия от Земята блясък на Марс.

Всички други фактори, от които блясъка на Марс зависи, не се променят, за това можем да не ги отчитаме.
За осветеността Е_М , която Марс създава върху можем да запишем следното:

Е_М ~ 1/(r_M².r_З-М²)

На сегашната орбита на Марс имаме, че: r_M = 1,524 AU , следователно в опозиция r_З-М = 0.524 AU.
След намесата на Михаела и Ивайло:
r_M = 1,041 AU , следователно в опозиция r_З-М = 0.041 AU.
Това означава, че разстоянието Марс – Слънце намалява 1,46 пъти, а разстоянието Земя – Марс – 12,8 пъти.
Следователно, блясъкът на Марс ще нарастне 350 пъти.
От тук получаваме, че ако m e звездната му величина при сегашно противостоене, то тогава тя ще бъде:
m₁ = m - 2,5.lg(350) ≈ -8^m
Това е наистина удивително! Веднага трябва да кажем на Михаела и Иво да се захващат за работа!
В случая когато Марс става вътрешна планета, минималното сближаване ще съответства на конфигурация долно съединение. Тогава към нас ще е обърната изцяло тъмната част на планетата. Поради това, осветеността, която Марс ще създава върху нас в този момент ще бъде равна на 0.

Критерии за оценяване
За напълно вярна задача, но без да е отчетен вторият случай се отнемат общо 4 т.
За правилен израз за синодичния период – 2 т.
За правилно изчислен сидеричен период – 1 т.
За съобразяване в каква конфигурация разстоянието е минимално – 1 т.
За правилно използване на третия закон на Кеплер – 1,5 т.
За правилно получена числена стойност – 0,5 т.
За правилно съобразяване на факторите от които зависи блясъкът на Марс и които се променят – 2т.
За правилна математическа постановка – 2т.
За правилен израз и вярна числена стойност – 1т.
За съобразяване на блясъка в случая за вътрешна планета – 1т.

3 задача. Астероид. Разполагаме с телескоп, с диаметър на обектива 60 см и фокусно разстояние 7 м, оборудван със CCD камера, имаща размер на пиксела 12 ?m и квантова ефективност 60%. С телескопа се наблюдава астероид от 18.5^m с голяма полуос на орбитата 4 AU и размери 10 kм, който е в опозиция, обикалящ по кръгова орбита около Слънцето.

• Каква е максималната продължителност на експозицията с която можем да снимаме астероида, така че образът му да не е размит върху кадъра?

• Ще можем ли да го регистрираме ако фонът на небето е равен на 20m/arcsec2?

• Обяснете качествено как влиянието на земната атмосфера би променило Вашия отговор.

Полезна информация:
- Квантовата ефективност се дефинира като частта от фотоните, които се регистрират от един приемник на светлина.
- Знаем, че от звездата Вега (0^m) всяка секунда пристигат 10 000 фотона на квадратен сантиметър.
- Считаме, че можем да регистрираме астероида ако от него са паднали поне 3 пъти повече фотони, отколкото от фона на небето.

Решение.
Астероидът е достатъчно голям и с достатъчно малки размери, за да считаме, че е точков източник на светлина.  Дифракционният лимит на телескопа е α″ = 14/D_[cm] = 0.23″, а мащабът на изображението δ = 206265″ d_px/F = 0.35″/px. Следователно ще считаме, че астероидът заема един пиксел върху CCD матрицата на телескопа.
Максималното време за експозиция ще бъде времето, за което астероидът преминава ъгловото разстояние, отговарящо на един пиксел – δ. Нека изчислим неговата ъглова скорост:

ω = Δv/r

където Δv е относителната линейна скорост между Земята и астероида, а r = 3 au, разстоянието между тях. За да намерим скоростта на астероида, първо ще изчислим периода му от третия закон на Кеплер:

а³/Т²= а_з³/Т_з²

където от лявата страна на уравнението стоят периодът и голямата полуос на астероида, а от дясната тези на Земята в години и астрономически единици респективно. Получаваме за периода на астероида Т = 8 години. Изчисляваме неговата орбитална скорост:

v = 2πa/T = 15 km/s
Δv = v_з – v

Максималното време на екзпозиция ще бъде:

t = δ/ω = d_px/Fω = d_pxr/FΔv = 51 s

За това време, астероидът ще измине един пиксел върху кадъра и няма да се размие. За толкова време, фотони от него ще попадат в един пиксел, а ако продължим екзпозицията те ще започнат  да попадат в съседния. Ако искаме да засечем астероида, няма смисъл да правим по-дълги експозиции, защото ако той не е засечен за това време, то при по-дълга екзпозиция той ще оставя същото количество фотони в съседни пиксели  и никога няма да остави сигнал по-голям от този на фона в даден пиксел. Единственото спасение е да настроим телескопа, така че той да следи не звездите, а самия астероид.
Нека все пак проверим дали експозицията от 51 s е достатъчна за неговото засичане.
Осветеността върху CCD матрицата се определя от броя засечени от нея фотони. Можем да запишем закона на Погсън в следния вид:

N_В/N_А = 2.512^Δm

където от ляво стоят броят фотони паднали от Вега и астероида на един квадратен сантиметър за секунда, а от дясно разликата в звездните им величини. Можем да изчислим, че от астероида всяка секунда идват приблизително 0.0004 фотона на кв. сантиметър (0.0004 ф.s^-1.cm^-2). От CCD камерата се засичат 60% от всички фотони попаднали върху огледалото на телексопа за определеното време на експонация.

N_Аtotal = N_A.(πD²/4).t.60% = 35 фотона

Сега да проверим колко фотона от небето ще попаднат върху същия и съседните пиксели. Аналогично изчисляваме, че от всяка квадратна дъгова секунда от небето идват N_небе=0.0001ф.s^-1.cm^-2.arcsec^-2. Тъй като небето, за разлика от астероида, е площен източник, то осветеността, която то ще създава върху камерата ще зависи от квадрата на светлосилата на телескопа D/F. Нека проверим как става това. Ъгловата площ, която вижда един пиксел от CCD камерата е δ² = d_px²/F². Пълният брой фотони попаднали от небето върху един пиксел ще бъде:

N_{небе total} =N_небе .(πD²/4).(d_px²/F²).t.60% = 1.1 фотона

Виждаме, че фотоните, попадащи от астероида са много повече, от тези попадащи от тъмното небе. Следователно  експозиция от 51 s ще бъде напълно достатъчна за засичането на този астероид.
Нека да дискутираме влиянието на земната атмосфера. Тя поглъща част от фотоните и размива изображението. Дифракционният лимит на телескопа беше около 0.23″/px. Такова изображение в редки случаи можем да получим само на най-добрите места за наблюдение от Земята – пустинята Атакама в Чили, Канарските или Хавайските острови. В повечето обсерватории обаче изображението е размито до 1 – 2 дъгови секунди. В такъв случай астероидът ще се разположи на няколко пиксела върху камерата и сигналът му ще падне (фонът на небето няма да се промени). За сметка на това, обаче ще можем да си позволим по-дълга експозиция, тъй като астероидът ще трябва да измине няколко пиксела преди да се размие.

Критерии за за оценяване
За изчисляване ъгловата скорост на астероида и максималната експозиция – 5 т.
За изчисляване колко фотона от астероида попадат във фокуса на телескопа – 5 т.
За изчисляване колко фотона попадат от небето – 5 т.
За коментари по влиянието на земната атмосфера – 2 т.

4 задача. Хладно Слънце. Да си представим, че на Слънцето се появява слънчево петно, което покрива цялата му повърхност. То има характерната за слънчевите петна температура около 4500 К.

• Как би се променила светимостта на Слънцето тогава в сравнение с настоящата му светимост?
• Може ли това състояние да продължи дълго, при положение, че няма промяна в процесите, които стават в ядрото на Слънцето? Обосновете вашия отговор.
• Нека приемем, че въпреки всичко температурата на повърхността на Слънцето остава понижена, но освобождаването на енергия в ядрото му продължава със сегашните си темпове, а Слънцето преминава към ново състояние на равновесие. Какво ще се промени, за да се постигне това ново равновесие? Направете количествени и качествени описания.
• Ще ни изглеждат ли променени цветовете и осветеността на предметите около нас? Дайте обяснение.

Решение.
Светимостта на една звезда се изразява чрез закона на Стефан-Болцман:

L = σT⁴.4πR²

Където Т е температурата, а R радиусът на звездата. Ако цялото Слънце се покрие с едно огромно петно, то неговата температура ще спадне до 4500 K. Тогава можем да запишем, че светимостта на Слънцето ще намалее:

L₁/L₂ = (T₁/T₂)⁴≈ 2.72 пъти

тъй като радиусът му не се променя.
Това състояние не може да продължи дълго, защото в ядрото на Слънцето продължава да се отделя енергия  със същия темп. Тази енергия трябва да има възможност да се отдели от повърхността му. За да стане това, то се раздува, за да компенсира ниската си температура. Радиусът, до който  ще се раздуе можем да намерим отново използвайки закона на Стефан-Болцман, като знаем, че светимостта му:

L₁/L₂ = (T₁/T₂)⁴(R₁/R₂)² = 1
R₁/R₂ = (T₁/T₂)² ≈ 1.65 пъти

За да продължи да съществува, покрито с огромното петно Слънцето трябва да увеличи радиуса си 1.65 пъти.
С по-ниска температура, максимумът на излъчване на Слънцето ще се премести към по-голяма дължина на вълната. Макар енергията, която достига Земята да остане същата, по-голяма част от фотоните ще бъдат в инфрачервената област и осветеността ще падне за човешкото око. Предметите ще ни изглеждат по-тъмни и по-червени. Допълнителен ефект, предизвикан от по-големите размери на звездата ни ще бъде, че сенките на предметите ще бъдат по-размити.

Критерии за оценяване:
За познаване на закона на Стефан-Болцман – 2 т.
За правилното му прилагане – 3 т.
За верни числени резултати – 3 т.
За описание на предметите – 2 т.

5 задача. Комета. Разглеждаме комета, която обикаля около Слънцето по елиптична орбита. Прекарваме права, лежаща в орбиталната равнина и минаваща през Слънцето. Правата разделя кометната орбита на две части. Да се докаже, че при каквато и да е ориентация на правата, когато кометата изминава всяка от двете части от орбитата си, тя получава еднакви общи количества слънчева енергия. Изменението на размера на ядрото и опашката на кометата в близост до Слънцето да не се отчита.

Решение:
На схемата е показана кометната орбита, като прекараната права я пресича в точките А и В, както е показано на схемата.

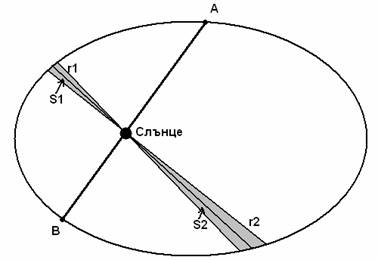
Разглеждаме два клонящи към нула времеви интервала Δt₁ и Δt₂ през които кометата изминава пътища, виждащи се под един и същи ъгъл от Слънцето.
Понеже тези два интервала са много малки, то можем да считаме, че по време на тях кометата остава на постоянни разстояния от Слънцето, които означаваме, съответно с r₁ и r₂. Отново, поради същата причина, можем да считаме, че скоростите й, v₁ и v₂ не се променят, а преместванията в двата случая са отсечки с дължини, съответно:

x₁ = v₁. Δt₁   и
x₂ = v₂. Δt₂.

Тъй като, тези премествания се виждат под един и същи ъгъл, то можем да запишем, че:

x₁ ~ r₁   и
x₂ ~ r₂.

За описваните от радиус – вектора комета – Слънце площи, можем да запишем:

S₁ ~ x₁.r₁ ~ r₁²   и
S₂ ~ x₂.r₂ ~ r₂².

Съгласно втория закон на Кеплер, кометата се движи по своята орбита с постоянна площна скорост, поради, което е в сила следното равенство:

S₁/S₂ = Δt₁ / Δt₂.

Следователно:

Δt₁ / Δt₂ =   r₁²/ r₂².

Енергиите, които кометата получава от Слънцето през двата интервала от време са пропорционални на произведенията на съответните осветености I1 и I2 и съответните интервали от време.
Но от друга страна можем да твърдим, че:

I₁ ~ 1/ r₁²    и
I₂ ~ 1/ r₂².

И така, за погълнатите енергии слънчева светлина получаваме:

E₁ ~ I₁. Δt₁    и
E₂ ~ I₂. Δt₂ .

Отношението им е:

E₁/E₂ =( I₁/I₂).(Δt₁/ Δt₂)=(r₂²/r₁²).(r₁²/r₂²) = 1.

По същия начин можем да разделим целите участъци, които кометата изминава. Сумарната енергия, която тя получава във всяка една от двете части на орбитата е сума от тези малки енергии, които се поглъщат от нея в съответните малки участъци. Следователно и сумарната енергия ще е една и съща.

Критерии за оценяване:
За правилен подход към задачата, чрез разделяне на двете части от орбитата й на малки частички – 4т.
За изразяване на отношението на лицата, чрез отношението на разстоянията – 3т.
За правилно прилагане на втория закон на Кеплер – 3т .
За правилно определяне на отношението на времевите интервали – 2т.
За изразяване на отношението на осветеностите – 2т.
За правилно съобразяване на количеството получена енергия – 2т.
За получаване, че енергиите са равни – 1т.