МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО
И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА
ПО АСТРОНОМИЯ
VІІІ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
http://astro-olymp.org
IІ кръг - решения
Ученици от 11-12 клас
1 задача. В двойната звездна система HD 48915 една от компонентите има видима звездна величина 8.44m и температура 25 000 К. Каква е тази звезда и къде се намира на диаграмата на Херцшпрунг-Ръсел? Обосновете вашия отговор с пресмятания. Паралаксът на двойната звезда е 0.379″.
Решение: Разстоянието да звездата е
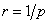
където p е паралаксът в дъгови секунди, а r се измерва в парсеци. За разстоянието получаваме 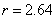 парсека, което означава, че това е една от най-близките до нас звезди. Видимият блясък на звездата, обаче, е много слаб. Звездната й величина парсека, което означава, че това е една от най-близките до нас звезди. Видимият блясък на звездата, обаче, е много слаб. Звездната й величина 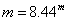 показва, че тя не се вижда с невъоръжено око. Следователно светимостта на звездата е много пъти по-ниска от тази на Слънцето. Същевременно виждаме, че звездата е много гореща – температурата й е Т = 25000 К. Оттук можем да направим извода, че звездата се намира в долната лява част на диаграмата на Херцшпрунг-Ръсел и представлява бяло джудже. Бихме могли да се досетим дори, че звездната система HD 48915 е Сириус и неговият спътник. показва, че тя не се вижда с невъоръжено око. Следователно светимостта на звездата е много пъти по-ниска от тази на Слънцето. Същевременно виждаме, че звездата е много гореща – температурата й е Т = 25000 К. Оттук можем да направим извода, че звездата се намира в долната лява част на диаграмата на Херцшпрунг-Ръсел и представлява бяло джудже. Бихме могли да се досетим дори, че звездната система HD 48915 е Сириус и неговият спътник. Да сравним светимостта на бялото джудже L със светимостта на Слънцето LS . Разстоянието от Земята до Слънцето е rS = 1 AU . Пресмятаме и разстоянието до звездата в астрономически единици:
r = 2.64 pc ×206265 AU ≈545000 AU
Да намерим видимата звездна величина m' , която звездата би имала, ако се намираше на разстояние от нас 1 AU . С Е означаваме осветеността, създавана на Земята от звездата, когато е на разтояние r от нас, а с Е' – осветеността, която тя би създавала, ако беше на разстоянието от нас до Слънцето rS , и пресмятаме:

Съгласно формулата на Погсон:


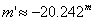
За светимостите на звездата и Слънцето можем да напишем:
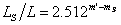
където mS = –26.74m е видимата звездна величина на Слънцето.
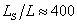
Следователно звездата е около 400 пъти по-слабо излъчваща от Слънцето.
А сега да сравним радиусите на звездата и на Слънцето. Приемайки, че Слънцето излъчва като абсолютно черно тяло, можем приблизително да изразим неговата светимост LS чрез температурата му ТS = 5800 К и радиуса RS със следното съотношение:
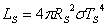 (1) (1)
където σ е константата на Стефан-Болцман. Аналогична формула можем да напишем и за звездата, означавайки с Т и R нейната температура и нейния радиус:
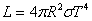 (2) (2)
Като разделим почленно тези съотношения, получаваме:

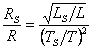

Звездата e около 370 пъти по-малка от Слънцето по размери, според нашата оценка. Обект с такива размери може да бъде бяло джудже.
По-точно определеният радиус на бялото джудже – спътник на Сириус, се оказва около 100 пъти по-малък от този на Слънцето. Получената тук от нас оценка е доста по-различна, макар и да е от същия порядък. Ето някои причини за неточността на нашия резултат:
• Използвайки формулите (1) и (2) за връзката между светимосттите, радиусите и температурите на бялото джудже и Слънцето, ние приемаме, че всеки от тези обекти излъчва като абсолютно черно тяло;
• В същите две формули по принцип трябва да фигурира болометричната светимост (светимостта в целия електромагнитен спектър), а нашите определения на светимостите се основават на звездните величини на звездите във видимата част от спектъра.
2 задача. Защо пълното лунно затъмнение може да трае повече от час, а пълното слънчево затъмнение – само няколко минути?
Решение: При пълно лунно затъмнение Луната преминава през земната сянка. Земята е около 3.5 пъти по-голяма от Луната по диаметър. Земната сянка с отдалечаване от Земята се стеснява, но на разстоянието на лунната орбита си остава все пак значително по-голяма от самата Луна. Докато Луната я прекоси, минава дълго време. При пълно лунно затъмнение сянката на Луната попада върху Земята. Тази сянка, обаче е най-много около 270 km . Скоростта, с която тя пробягва по земната повърхност е различна, но е сравнима с линейната скорост на Луната по нейната орбита. Ето защо времето, за което даден пункт от земната повърхност остава в границите на лунната сянка, е само няколко минути.
3 задача.
 Основните планетни конфигурации на външните планети със Земята и Слънцето са следните: съединение, опозиция (противостояние), източна квадратура и западна квадратура. Основните планетни конфигурации на външните планети със Земята и Слънцето са следните: съединение, опозиция (противостояние), източна квадратура и западна квадратура.
• Обозначете четирите конфигурации на схемата.
• Посочете в каква последователност се изреждат те във времето.
• За кои външни планети конфигурациите се случват през по-кратки интервали от време – за планетите с по-близки орбити до нас, или с по-далечни?
Решение:
 Конфигурациите се обозначават, както е показано на чертежа. Нека предположим, че планетата първо се наблюдава в опозиция, т.е. на 180 ° от Слънцето. Съгласно ІІІ закон на Кеплер, външните планети се движат около Слънцето по-бавно от Земята. Това означава, че след опозицията планетата ще изостава от Земята и следващата конфигурация, която ще се наблюдава, ще бъде източна квадратура. За земните наблюдатели планетата ще бъде на 90 ° източно от Слънцето. Изоставането на планетата относно Земята ще продължи и видимото й положение на небето за земните наблюдатели все повече ще се приближава към Слънцето. Следващото положение, в което ще се наблюдава планетата, ще бъде съединение със Слънцето. След него ще последва западната квадратура и после отново опозиция. Последователността е опозиция, източна квадратура, съединение, западна квадратура. Конфигурациите се обозначават, както е показано на чертежа. Нека предположим, че планетата първо се наблюдава в опозиция, т.е. на 180 ° от Слънцето. Съгласно ІІІ закон на Кеплер, външните планети се движат около Слънцето по-бавно от Земята. Това означава, че след опозицията планетата ще изостава от Земята и следващата конфигурация, която ще се наблюдава, ще бъде източна квадратура. За земните наблюдатели планетата ще бъде на 90 ° източно от Слънцето. Изоставането на планетата относно Земята ще продължи и видимото й положение на небето за земните наблюдатели все повече ще се приближава към Слънцето. Следващото положение, в което ще се наблюдава планетата, ще бъде съединение със Слънцето. След него ще последва западната квадратура и после отново опозиция. Последователността е опозиция, източна квадратура, съединение, западна квадратура.
Колкото по-далечна от Слънцето е една планета, толкова по-бавно се движи тя около Слънцето. Следователно темпът на изоставане на планетата от Земята при движението й по орбитата ще бъде по-голям. Ето защо при по-далечните планети редуването на конфигурациите в установената последователност ще става през по-кратки интервали от време.
4 задача. Звездният куп Плеяди е един от най-близките до нас разсеяни звездни купове и с невъоръжено око в него могат да се различат отделни звезди. Видимите звездни величини на седемте най-ярки звезди от Плеядите са 2.9m , 3.6m , 3.7m , 3.9m , 4.2m , 4.3m и 5.1m . Каква би била видимата звездна величина на една звезда с блясък, равен на общия блясък на седемте звезди?
Решение: Да означим с m1 , m2, m3, m4, m5, m6 и m7 звездните величини на звездите, а с m – звездната величина на хипотетичната звезда с общия им блясък. Съответно с Е1 до Е7 означаваме осветеностите, които звездите създават за земния наблюдател, а с Е – осветеността, създавана от хипопетичната звезда. По условие:
Е = Е1 + Е2 + Е3 + Е4 + Е5 + Е6 + Е7 (1)
За първата звезда по формулата на Погсон можем да напишем:
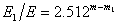

Аналогични съотношения можем да напишем и за всяка от другите звезди и като ги заместим в (1), получаваме:
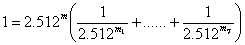

m ≈ 1.67m
5 задача. Радиусът на една звезда – бяло джудже, е равен на радиуса на Земята, а масата й е равна на масата на Слънцето. Ако на Земята теглото ни е 50 kg , то на повърхността на бялото джудже бихме тежали 15 000 000 kg !
Ако наистина попаднем върху такова бяло джудже, ще прибавим ли 15 000 000 kg към неговата маса? Обяснете своя отговор.
Когато космическата совалка стартира от Земята, теглото на космонавтите в нея се увеличава 5 пъти. Ако совалката излита от бялото джудже със същото ускорение, колко пъти ще се увеличи теглото на космонавтите в нея? (Пресметнете отговора само теоретично, макар да е ясно, че нито космонавтите, нито совалката могат да оцелеят там).
Решение: Тегло на едно тяло се нарича гравитационната сила (силата на тежестта), с която Земята привлича тялото. Вследствие на гравитационното привличане на Земята тялото, поставено върху хоризонтална опора, оказва върху нея натиск. Натискът, приложен върху опората, е равен по големина на теглото на тялото. Обикновените пружинни кантари, върху които стъпваме, за да измерим собственото си тегло, са конструирани така, че показанията им са пропорционални именно на този натиск. Ако нашата маса е m = 50 kg , то силата на тежестта, с която ни действа Земята, ще бъде
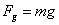
където g е ускорението на силата на тежестта на земната повърхност. Силата на тежестта, която би ни действала на бялото джудже, ще бъде

където g1 е ускорението на силата на тежестта на неговата повърхност. Равен по големина ще бъде и натискът, който там бихме оказвали върху повърхността. Щом теглото ни, измерено на бялото джудже, би било 15 000 000 kg , то това означава, че
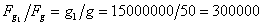
или на бялото джудже ще ни действа 300 000 пъти по-голяма сила на тежестта, отколкото на Земята. Т.е. там ускорението на силата на тежестта е 300 000 пъти по-голямо, отколкото на Земята. Затова ние бихме оказвали 300 000 пъти по-силен натиск върху въображаемия кантар, с който мерим теглото си. Това, обаче, не променя нашата маса, която си остава 50 kg , и ние бихме прибавили към масата на бялото джудже именно 50 kg , а не 15 000 000 kg. Наистина, ако решим да се претеглим не с кантар от гореспоменатия вид, а с везна, то теглилката, с която бихме уравновесили теглото си, би била с маса също 50 kg , а не 15 000 000 kg . Естествено, всички тези разсъждения се отнасят само до мислени опити, защото при такава сила на привличане на повърхността на бялото джудже нашите тела, както и всякакви измервателни уреди биха били напълно смазани и разрушени.
Когато космическата совалка стартира от Земята, теглото на космонавтите е пропорционално на сумата от земното ускорение (ускорението на силата на тежестта на земната повърхност) g и на ускорението а , с което совалката се движи нагоре. Щом теглото на космонавтите се увеличава 5 пъти в сравнение с нормалното им тегло, то:
5 mg = m ( a + g )
Следователно:
a = 5 g – g = 4 g
При опит совалката да стартира от повърхността на бялото джудже със същото ускорение, теглото на космонавтите ще бъде пропорционално на сумата от ускорението на силата на тежестта на повърхността на бялото джудже g1 и а . Но g1 = 300000 g , а а = 4 g . Следователно при излитане на совалката от бялото джудже със същото ускорение, теглото на космонавтите би се увеличило с пренебрежимо малка стойност.
Справочни данни за всички възрастови групи:
Наклон на лунната орбита към равнината на земната орбита 5 ° 09'
Средно разстояние от Земята до Слънцето 1 AU = 150000000 km
Видима звездна величина на Слънцето –26.74m
Температура на Слънцето 5800 К |