МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА ПО АСТРОНОМИЯ
ІХ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
http://astro-olymp.org
ІІІ кръг - задачи и решения
Ученици от 9-10 клас
1 задача. На снимката виждате негативно изображение на слънчева аналема. Тя се получава, когато в продължение на една година, през няколко дни, в един и същи час, Слънцето бива снимано, като при всеки кадър, с голяма прецизност, се възпроизвежда една и съща ориентация на фотокамерата.
- В колко часа местно време е била снимана тази аналема?
- Означете с кръгчета и местата, където Слънцето се е намирало по време на равноденствията и слънцестоянията. До тях напишете датите когато това се е случило.
- Със стрелки означете посоките в които Слънцето се “придвижва” по аналемата.
- Каква е приблизителната географска ширина на която е направена тази снимка?
Решение:
Аналемата се дължи на това, че Слънцето не се движи по небесния екватор, а по еклиптиката, която е наклонена спрямо екватора под ъгъл 23°.5. Освен това, поради ексцентрицитета на Земната орбита, движението по еклиптиката е неравномерно. Официалното време се определя от така нареченото “средно Слънце”, което равномерно се ”движи” по небесния екватор. Истинското Слънце, в продължение на една година, изостава или избързва спрямо средното, издига се по деклинация, или слиза надолу.
Както е известно от уравнението на времето, максималните отклонения от нулевата линия по ректасценция са около 16.5 минути, което в ъглова мярка е около 4°. По деклинация, обаче, Слънцето се отклонява от средното слънце на 23°.5. Поради това аналемата представлява силно изтеглена по деклинация фигура. Почти на върховете на осморката Слънцето се отдалечава максимално от небесния екватор. Там се намират точките на лятно и зимно слънцестоене и щом осморката е изправена, то аналемата е композирана около местно пладне (виж рисунката).
Както вече споменахме, Слънцето е в точките на слънцестоене близо до върховете на аналемата. Тогава то има и максимална, респективно - минимална деклинация. Следователно почти точно по средата, между върховете на аналемата, Слънцето е в равноденствените си точки. Поради асиметрията в движението на истинското Слънце, равноденствените точки не съвпадат с възела на аналемата.
Асиметрията на аналемата се дължи на това, че Земята се движи по елиптична орбита. Около 10 дни след зимното (за нас) слънцестоене, в началото на януари, Земята преминава през перихелия на своята орбита, поради което Слънцето напредва значително по еклиптиката и изпреварва бързо “средното слънце”. Освен това, тогава Слънцето се движи почти успоредно на небесния екватор. Ето защо в месеците около перихелия се оформя най-широката част на аналемата. На снимката виждаме, че по-широката част е отгоре на аналемата. Това означава че през месеците декември и януари Слънцето е най-високо над хоризонта и следователно аналемата е правена в Южното полукълбо. Следователно изток е надясно и при бързото нарастване на ректасцензията на Слънцето, то се придвижва в горната част на аналемата надясно. След това тръгва надолу и наляво. после, близо до лятното слънцестоене Земята е близо до своя афелий и би трябвало да изостава спрямо средното слънце. Това, обаче, се компенсира изцяло от факта, че тогава Слънцето се движи по еклиптиката успоредно на небесния екватор. Като резултат, в най – ниската си точка, Слънцето отново се придвижва на изток, макар и по-слабо.
Височината на аналемата е 47°. На изображението аналемата е висока 178 мм. Долният край на аналемата е на 80 мм от хоризонта, което отговаря на 21°.1 . Небесният екватор е на още 23°.5 нагоре. Максималната височина на екватора над хоризонта е 44°.6. Следователно географската ширина на мястото е :
φ = 90° - 44°.62 = 45°. 4 южна ширина
2 задача. През 2004 година наблюдавахме рядко астрономическо явление – преминаване (пасаж) на Венера пред видимия слънчев диск. Възможно е също и покритие на Венера от Слънцето.
Оценете времето, за което при покритие на Венера от Слънцето, видимият диск на Венера се скрива зад края на слънчевия диск, т.е. времето от първия до втория контакт. Приемете, че покритието е централно.
Пояснение: Първи контакт е моментът в началото на покритието, в който видимият диск на Венера за първи път се допира външно към видимия диск на Слънцето. Втори контакт е моментът, в който започва пълното покритие на Венера, или нейният видим диск за първи път изцяло се е скрил зад видимия слънчев диск.
Справочни данни:
Радиус на орбитата на Земята около Слънцето – 150 000 000 км
Радиус на орбитата на Венера около Слънцето – 108 000 000 км
Радиус на Венера – 6 050 км
Решение:
Означаваме радиусите на орбитити на Земята и Венера съответно с а и а1 , а орбиталните им периоди – с Т и Т1. От ІІІ закон на Кеплер намираме орбиталния период Т1 на Венера около Слънцето:

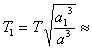 0.611 години 0.611 години
І начин. 
При покритието на Венера от Слънцето планетата започва да навлиза зад видимия слънчев диск от западната му страна. Да си представим права линия, минаваща през земния наблюдател и допирателна към западната страна на Слънцето. Поради движението на Земята около Слънцето, тази линия също се движи. Тя се върти с ъглова скорост, равна на ъгловата скорост w на Земята около Слънцето.

Центърът на въртене е точка от повърхността на Слънцето. Поради малките размери на Слънцето и на Венера в сравнение с разстоянието до Венера, може да приемем, че центърът на въртене е в центъра на Слънцето.
Ъгловата скорост на Венера спрямо Слънцето е

Ъгловата скорост на Венера спрямо линията Земя–Слънце е:

Тогава времето за пресичане на тази линия от Венера е равно на ъгловите размери на планетата a , спрямо центъра на Слънцето, разделени на получената ъглова скорост:
 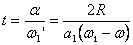
където R е радиусът на Венера.
Окончателно получаваме:

 min min
Същото може да се получи и така:
Линейната скорост на пресечната точка на тази права с орбитата на Венера е:
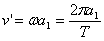
Линейната скорост на самата Венера по нейната орбита е:
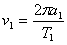
Относителната скорост, с която се движи Венера спрямо пресечната точка на въртящата се права линия с орбитата на планетата е:

Тогава търсеното от нас време за скриване на видимия диск на Венера зад Слънцето е:

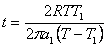
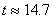 min min
ІІ начин:
В горно съединение относителната линейна скорост на Венера спрямо Земята е:
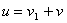
където 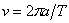 и и  са съответно линейните скорости на Земята и на Венера по техните орбити. Видимата ъглова скорост на Венера на фона на звездите за земния наблюдател ще бъде: са съответно линейните скорости на Земята и на Венера по техните орбити. Видимата ъглова скорост на Венера на фона на звездите за земния наблюдател ще бъде:
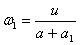
Видимата ъглова скорост на Венера относно Слънцето за земния наблюдател ще бъде:
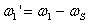
където  е ъгловата скорост на годишното движение на Слънцето по еклиптиката. е ъгловата скорост на годишното движение на Слънцето по еклиптиката.
Търсеното време за скриването видимия диск на Венара зад Слънцето е:

Като заместим стойностите от горните равенства, получаваме:

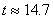 min min
3 задача. Замечтан метеорен наблюдател гледа звездното небе и си мисли за едно желание. Дълго време не може да си го пожелае, защото не се появяват метеори. Вместо тях, при него идва добра вълшебница и му предсказва, че желанието ще се сбъдне. После леко излита нагоре и миг преди да изчезне, пуска облак от милион частици звезден прах. Звездната величина на облака е 3 m . Малко по-късно една прашинка пада в ръката на наблюдателя и от разстояние 30 см свети за него като звездичка от 3-та звездна величина.
- На каква височина е изчезнала вълшебницата?
- При появата си облакът по своята повърхностна яркост е подобен на Млечния път. Колко пъти се е изменила тази яркост, когато облакът се е спуснал на половината от първоначалната си височина?
Виж вълшебницата, нарисувана от Десислава Живкова, участничка в олимпиадата.
Решение:
Щом облакът е от милион (1 000 000) частици, значи на разстояние 30 см от наблюдателя целият облак би имал 1 000 000 пъти по-силен видим блясък, отколкото една своя частица. На височината Н , на която е изчезнала вълшебницата, целият облак е имал същия видим блясък
(3 m ), както една прашинка на разстояние 30 см . Следователно на височината Н облакът е имал видим блясък, 1 000 000 пъти по-слаб, отколкото би имал на разстояние 30 см . Видимият блясък на един светещ обект е обратно пропорционален на квадрата на разстоянието до него. Ето защо височината Н трябва да е 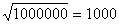 пъти по-голяма от 30 см , или Н = 300 метра . пъти по-голяма от 30 см , или Н = 300 метра .
Повърхностната яркост на един светещ обект е осветеността, създавана от единица площ на обекта, изразена в ъглови мерки (примерно квадратни градуси). При приближаване на обекта към наблюдателя, общият му блясък ще нараства обратно пропорционално на разстоянието до него. Същевременно, обаче, ще се увеличава неговата видима площ в ъглови мерки. Това увеличение ще бъде също обратно пропорционално на квадрата на разстоянието до обекта. Така че, в крайна сметка повърхностната яркост на обекта ще остава неизменна, защото увеличеният общ блясък на обекта ще се разпределя върху също толкова пъти по-голяма видима ъглова площ. В заключение, когато облакът от звезден прах се е спуснал на половината от първоначалната си височина, той също ще е бил подобен по повърхностна яркост на Млечния път, само че ще бъде с по-голям видим размер. 4 задача. На рисунката виждате диаграма, показваща видимите положения на четирите галилееви спътника на Юпитер – Йо, Европа, Ганимед и Калисто. Като използвате данните от диаграмата, направете подходящи измервания и определете възможно най-точно масата на планетата Юпитер.
Ако сте наблюдавали с телескоп Юпитер в 0 h на днешния ден, как би бил разположен относно планетата всеки един от спътниците? Нарисувайте схема.
Орбиталното движение на Юпитер, както и това на Земята да не се отчита.
Справочни данни:
гравитационна константа γ = 6.67×10-11 m3 / kg . s2
Радиус на Юпитер 71 500 км
Решение:
Определяме мащабите на скалите на диаграмата. По скалата на разстоянията на 80 радиуса на Юпитер отговарят 82 мм. Мащабът е 80/82 » 0.9756 радиуса на Юпитер на милиметър. По скалата на времето на 40 дни отговарят 151 мм. Мащабът е 40/151 » 0.265 денонощия на милиметър.
Измерваме амплитудите на изменение на разстоянията от спътниците до центъра на Юпитер. Това са радиусите на орбитите на спътниците около Юпитер. За по-точни резултати амплитудата на изменение на разстоянието до Юпитер измерваме на няколко места и усредняваме резултатите. Получаваме:
| Спътник |
Радиус на орбитата r00
в мм |
Радиус на орбитата
в радиуси на Юпитер,
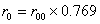 рад.юп./мм рад.юп./мм |
| Йо |
6 |
5.8536 |
| Европа |
9.5 |
9.2682 |
| Ганимед |
15 |
14.634 |
| Калисто |
27 |
26.3412 |
За да определим по-точно орбиталния период на даден спътник, измерваме общата продължителност на колкото е възможно повече периоди върху диаграмата и делим получената стойност на броя периоди. Например за Йо можем да измерим общата продължителност на 21 периода, за Европа – 10, за Ганимед – 5 и за Калисто – 2 периода. Резултатите са следните:
| Спътник |
Орбитален период Т00
в мм |
Орбитален период в денонощия,
 дни/мм дни/мм |
| Йо |
6,68 |
1.7702 |
| Европа |
13,4 |
3.551 |
| Ганимед |
27 |
7.155 |
| Калисто |
62,5 |
16.5625 |
От ІІІ закон на Кеплер:

където М е масата на Юпитер, а е радиусът на орбитата на спътника, Т е неговият орбитален период, а γ е гравитационната константа. Масата на Юпитер е:

Чрез умножаване по радиуса на Юпитер в километри, превръщаме радиусите на орбитите на спътниците също в километри, а после и в метри. Превръщаме стойностите на орбиталните периоди от денонощия в секунди и заместваме в горната формула. За масата на Юпитер от данните за различните спътници получаваме:
| Спътник |
Маса на Юпитер |
Йо |
1.853×1027 kg |
Европа |
1.828×1027 kg |
Ганимад |
1.773×1027 kg |
Калисто |
1.929×1027 kg |
Окончателно масата на Юпитер получаваме, като средно аритметично на тези резултатите – 1. 846×1027 kg .
Като пресечем диаграмата с хоризонтална линия, съответстваща на 0 h за датата на ІІІ кръг на астрономическата олимпиада (13 май), виждаме, че на този ден спътникът Европа е на изток от Юпитер, а Йо, Ганимед и Калисто са на запад, както е показано на схемата.
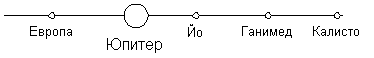
Спътниците разпознаваме по това, че в реда Йо, Европа, Ганимед, Калисто, те са подредени по нарастване на отдалечеността им от Юпитер.
|