МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА ПО АСТРОНОМИЯ
ІХ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
http://astro-olymp.org
ІІІ кръг - задачи и решения
Ученици от 11-12 клас
1 задача. В 1987 г . в Големия магеланов облак – галактика-спътник на нашия Млечен път – избухна свръхнова звезда, която беше видима с невъоръжено око. По-късно в мъглявината, останала след взрива, беше открит необикновеният обект, в който се е превърнала звездата – пулсар, излъчващ импулси през интервал само около 0.0005 секунди. Според съвременната теория, пулсарите са свръхплътни неутронни звезди с изключително силни магнитни полета, които се въртят много бързо.
Като приемете, че даденият период на импулсите е равен на периода на околоосно въртене на пулсара, докажете, че той трябва да е обект с много висока плътност.
Справочни данни:
Гравитационна константа γ = 6.67×10-11 m3 / kg . s2
Решение:
При период на въртене  секунди, скоростта на околоосно движение за точка от екватора на обекта ще бъде секунди, скоростта на околоосно движение за точка от екватора на обекта ще бъде  , където R е неговият радиус. В координатна система, въртяща се заедно с пулсара, на елемент от неговата повърхност с маса m ще действа центробежна сила , където R е неговият радиус. В координатна система, въртяща се заедно с пулсара, на елемент от неговата повърхност с маса m ще действа центробежна сила
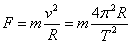
За да не се разруши пулсарът под действие на центробежните сили, необходимо е те да не надвишават силите на гравитационно привличане в него. На същия елемент от повърхността действа сила на привличане:
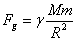
където M е масата на пулсара, а 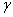 е гравитационната константа. Сравняваме двете сили и изразяваме масата чрез обема и плътността е гравитационната константа. Сравняваме двете сили и изразяваме масата чрез обема и плътността  на въртящия се обект ( на въртящия се обект ( ), получаваме: ), получаваме:
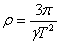
 kg / m3 kg / m3
Получената оценка е за минималната стойност на плътността, при която обектът не би се разрушил от центробежните сили при въртенето. Стойността е впечатляващо голяма, по-голяма дори и от типичните плътности, каквито се смята, че трябва да имат неутронните звезди. Затова този обект е особено интересен за астрономите. Предполага се, че веществото в него дори не би могло да е само от неутрони, а да се намира в още по-необикновено и непознато на науката състояние и да се състои от по-екзотични частици (например кварки).
2 задача. През 2004 година наблюдавахме рядко астрономическо явление – преминаване (пасаж) на Венера пред видимия слънчев диск. Възможно е също и покритие на Венера от Слънцето.
Оценете времето, за което при покритие на Венера от Слънцето, видимият диск на Венера се скрива зад края на слънчевия диск, т.е. времето от първия до втория контакт. Приемете, че покритието е централно.
Пояснение: Първи контакт е моментът в началото на покритието, в който видимият диск на Венера за първи път се допира външно към видимия диск на Слънцето. Втори контакт е моментът, в който започва пълното покритие на Венера, или нейният видим диск за първи път изцяло се е скрил зад видимия слънчев диск.
Справочни данни:
Радиус на орбитата на Земята около Слънцето – 150 000 000 км
Радиус на орбитата на Венера около Слънцето – 108 000 000 км
Радиус на Венера – 6 050 км
Решение:
Означаваме радиусите на орбитити на Земята и Венера съответно с а и а1 , а орбиталните им периоди – с Т и Т1. От ІІІ закон на Кеплер намираме орбиталния период Т1 на Венера около Слънцето:

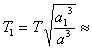 0.611 години 0.611 години
І начин. 
При покритието на Венера от Слънцето планетата започва да навлиза зад видимия слънчев диск от западната му страна. Да си представим права линия, минаваща през земния наблюдател и допирателна към западната страна на Слънцето. Поради движението на Земята около Слънцето, тази линия също се движи. Тя се върти с ъглова скорост, равна на ъгловата скорост w на Земята около Слънцето.

Центърът на въртене е точка от повърхността на Слънцето. Поради малките размери на Слънцето и на Венера в сравнение с разстоянието до Венера, може да приемем, че центърът на въртене е в центъра на Слънцето.
Ъгловата скорост на Венера спрямо Слънцето е

Ъгловата скорост на Венера спрямо линията Земя–Слънце е:

Тогава времето за пресичане на тази линия от Венера е равно на ъгловите размери на планетата a , спрямо центъра на Слънцето, разделени на получената ъглова скорост:
 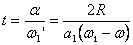
където R е радиусът на Венера.
Окончателно получаваме:

 min min
Същото може да се получи и така:
Линейната скорост на пресечната точка на тази права с орбитата на Венера е:
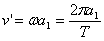
Линейната скорост на самата Венера по нейната орбита е:
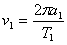
Относителната скорост, с която се движи Венера спрямо пресечната точка на въртящата се права линия с орбитата на планетата е:

Тогава търсеното от нас време за скриване на видимия диск на Венера зад Слънцето е:

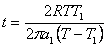
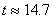 min min
ІІ начин:
В горно съединение относителната линейна скорост на Венера спрямо Земята е:
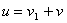
където 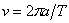 и и  са съответно линейните скорости на Земята и на Венера по техните орбити. Видимата ъглова скорост на Венера на фона на звездите за земния наблюдател ще бъде: са съответно линейните скорости на Земята и на Венера по техните орбити. Видимата ъглова скорост на Венера на фона на звездите за земния наблюдател ще бъде:
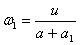
Видимата ъглова скорост на Венера относно Слънцето за земния наблюдател ще бъде:
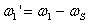
където  е ъгловата скорост на годишното движение на Слънцето по еклиптиката. е ъгловата скорост на годишното движение на Слънцето по еклиптиката.
Търсеното време за скриването видимия диск на Венара зад Слънцето е:

Като заместим стойностите от горните равенства, получаваме:

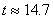 min min
3 задача. Вие участвате в пилотиран полет до Марс с минимален разход на гориво. От Земята вашият космически кораб тръгва по елиптична орбита около Слънцето с перихелий върху орбитата на Земята и афелий върху орбитата на Марс. Изминавайки половината от тази елипса, корабът достига до червената планета. След известен престой на Марс корабът се връща на Земята, като тръгва отново по елипса със същите характеристики. Приемете, че Земята и Марс се движат по кръгови орбити около Слънцето.
- Колко време ще трае полетът до Марс?
- В каква позиция трябва да бъде Марс относно Земята в началото на пътешествието?
- Колко време трябва да бъде престоят на космонавтите на повърхността на планетата, докато настъпи подходящият момент, когато могат да тръгнат обратно към Земята?
- Колко време ще трае общо цялото пътешествие?
Справочни данни:
Радиус на орбитата на Марс 1.5237 AU (астрономически единици)
Решение:

От чертежа става ясно, че корабът ще се движи по елипса с голяма полуос, равна на половината от сумата на радиусите на земната и марсианската орбита aT и aM . Орбиталния период Т на движение по тази елипса определяме от ІІІ закон на Кеплер:
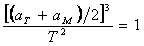
където aT и aM се измерват в астрономически единици, а Т в земни години.
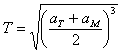
Времето t за достигане на кораба от Земята до Марс ще бъде само половината от орбиталния период Т , защото корабът изминава само половината от елиптичната траектория.
 години години
Когато корабът стигне до марсианската орбита, планетата Марс трябва да бъде там, в точка Марс 2. Моментът на изпращането на кораба от Земята е бил  0.7087 години по-рано. За това време Марс трябва да е изминал дъга от своята орбита, съответстваща на ъгъл: 0.7087 години по-рано. За това време Марс трябва да е изминал дъга от своята орбита, съответстваща на ъгъл:
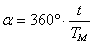
където 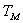 е сидеричният период на обикаляне на Марс около Слънцето. Можем да го намерим в години също от ІІІ закон на Кеплер: е сидеричният период на обикаляне на Марс около Слънцето. Можем да го намерим в години също от ІІІ закон на Кеплер:

Накрая получаваме 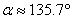 . В момента на тръгването на кораба от Земята Марс е бил в положение Марс 1, на ъгъл 135.7° назад по орбитата си от положение Марс 2, където е станала срещата с кораба. . В момента на тръгването на кораба от Земята Марс е бил в положение Марс 1, на ъгъл 135.7° назад по орбитата си от положение Марс 2, където е станала срещата с кораба.
За времето t , през което е траел полетът до Марс, Земята се е преместила до положение Земя 2, което е на ъгъл β от първоначалното Земя 1. Намираме този ъгъл:

Тук ТТ е орбиталният период на Земята.
При завръщането си към Земята корабът ще лети по елипса със същите параметри, както при пътуването от Земята до Марс. Следователно полетът на връщане също ще трае време t . За да срещнем Земята, когато достигнем до земната орбита, трябва правилно да сме избрали момента за тръгването си от Марс. Точката, в която достигаме Земята на нейната орбита, е противоположна на точката, в която се намира Марс при излитането ни от него. Т.е. тогава Земята трябва да е на 180° от Марс. Земята изпреварва Марс при движението си около Слънцето. За време t тя изминава 255.1° от орбитата си. Ето защо, когато тръгваме от Марс, Земята трябва да е на 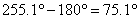 назад от Марс по посоката на обикаляне около Слънцето. В момента на нашето пристигане на Марс, обаче, Земята е на назад от Марс по посоката на обикаляне около Слънцето. В момента на нашето пристигане на Марс, обаче, Земята е на 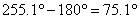 пред Марс. За да бъде в желаната от нас позиция спрямо Слънцето (75.1° след него), Земята трябва да го изпревари с пред Марс. За да бъде в желаната от нас позиция спрямо Слънцето (75.1° след него), Земята трябва да го изпревари с 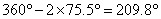 . Това може да стане след време: . Това може да стане след време:

където TMsyn е синодичният период на Марс. Определяме го от формулата:
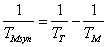
Заместваме и получаваме:
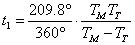
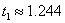 години години
Такъв ще бъде престоят на земната експедиция на Марс. Накрая общо цялото пътешествие ще продължи:
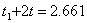 години ≈ 2 години 8 месеца. години ≈ 2 години 8 месеца.
4 задача. Разполагате със схема на разсеяния звезден куп Хияди, на която, освен звездите, са нанесени векторите на собствените движения на звездите от района на купа. В таблицата са дадени лъчевите скорости и собствените движения на 10 избрани звезди, принадлежащи на звездния куп. Съществува метод за определяне на разстоянията до движещи се купове, според който е достатъчно да знаем лъчевите скорости и собствените движения на звездите, както и ъгловите им разстояния до радианта на купа, т.е. точката в пространството, от която или към която всички звезди от купа се движат.
- Изведете формула, свързваща тези величини. В нея нека лъчевите скорости бъдат в [km/s], собствените движения в дъгови секунди на година, а разстоянието да се получава в парсеци.
- От схемата на купа продължете векторите на собствените движения на
10 – 15 звезди до пресичането им в една неголяма област. Приемете, че центърът на тази област е радианта на купа.
- Обърнете внимание, че системата от векторите е леко извита! Защо е така?
- Внимателно определете ъгловите разстояния от радианта на купа до всяка една от подбраните звезди. Пресметнете, по получената от вас формула, разстоянието до всяка от избраните звезди и намерете средната величина, която е търсеното разстояние до звездния куп.
Решение:
Ъгълът между радианта на купа и посоката към една звезда от него е всъщност ъгълът между зрителния лъч и пространствената скорост на звездата. Тогава очевидно връзката между тангенциалната скорост и радиалната скорост е:

където φ е ъгловото разстояние от радианта до съответната звезда.
Собственото движение, изразено в [arcsec/sec] e:
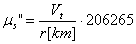
където 206265 е броят на дъговите секунди в един радиан, а Vt е в [km/s].
Собственото движение, изразено в [arcsec/год] e :

където n е броят на секундите в една година.
Разстоянието в парсеци е:
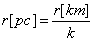
където k е броят на километрите в един парсек.
Получаваме:
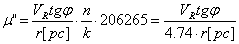
От тук следва:
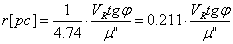
Това е формулата за пресмятане на разстоянията до звездите.
Дъгите, които свързват звездите с радианта на купа, са части от голям кръг. За разлика от тях небесните паралели са малки кръгове и в проекция върху равнината са извити в посока към небесния екватор. На схемата, обаче, паралелите са представени с прави линии и затова, по отношение на тях, големите кръгове са извити в противоположна посока.
При построяването на продълженията на векторите е добре това да се има предвид, защото в противен случай разстоянието до радианта ще бъде леко увеличено, което от своя страна, поради това, че ъгълът е аргумент на тангенсова функция, ще доведе до значително надценяване на разстоянието до купа. Определяме област с размери около 9 градуса за област на радиация и приемаме центъра й за вероятен радиант на Хиядите (виж схемата). Забелязваме, че мащабът по двете оси е различен, но ако той се коригира, продълженията на векторите ще станат още по-близки, по направление, до небесния екватор. Затова не обръщаме внимание на лекия наклон на векторите и измерваме разстоянията в мащаба на абсцисната ос. Нанасяме получените резултати в таблицата и по формулата пресмятаме разстоянията до звездите. Намираме средно аритметичната стойност, за която получаваме:

което е една добра оценка за разстоянието до купа.
|